题目内容
【题目】如图，是将抛物线y=﹣x2平移后得到的抛物线，其对称轴为x=1，与x轴的一个交点为A（﹣1，0），另一个交点为B，与y轴的交点为C．
（1）求抛物线的函数表达式；
（2）若点N为抛物线上一点，且BC⊥NC，求点N的坐标；
（3）点P是抛物线上一点，点Q是一次函数y= 
x+ 的图象上一点，若四边形OAPQ为平行四边形，这样的点P、Q是否存在？若存在，分别求出点P，Q的坐标；若不存在，说明理由．
【答案】
（1）
解：设抛物线的解析式是y=﹣（x﹣1）2+k．
把（﹣1，0）代入得0=﹣（﹣1﹣1）2+k，
解得k=4，
则抛物线的解析式是y=﹣（x﹣1）2+4，即y=﹣x2+2x+3；
（2）
解：在y=﹣x2+2x+3中令x=0，则y=3，即C的坐标是（0，3），OC=3．
∵B的坐标是（3，0），
∴OB=3，
∴OC=OB，则△OBC是等腰直角三角形．
∴∠OCB=45°，
过点N作NH⊥y轴，垂足是H．
∵∠NCB=90°，
∴∠NCH=45°，
∴NH=CH，
∴HO=OC+CH=3+CH=3+NH，
设点N纵坐标是（a，﹣a2+2a+3）．
∴a+3=﹣a2+2a+3，
解得a=0（舍去）或a=1，
∴N的坐标是（1，4）；
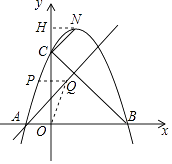
（3）
解：∵四边形OAPQ是平行四边形，则PQ=OA=1，且PQ∥OA，
设P（t，﹣t2+2t+3），代入y= 
x+ ，则﹣t2+2t+3= （t+1）+ ，
整理，得2t2﹣t=0，
解得t=0或 
．
∴﹣t2+2t+3的值为3或 
．
∴P、Q的坐标是（0，3），（1，3）或（ ， ）、（ ， ）．
【解析】（1）已知抛物线的对称轴，因而可以设出顶点式，利用待定系数法求函数解析式；（2）首先求得B和C的坐标，易证△OBC是等腰直角三角形，过点N作NH⊥y轴，垂足是H，设点N纵坐标是（a，﹣a2+2a+3），根据CH=NH即可列方程求解；（3）四边形OAPQ是平行四边形，则PQ=OA=1，且PQ∥OA，设P（t，﹣t2+2t+3），代入y= x+ ，即可求解．
