题目内容
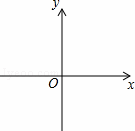
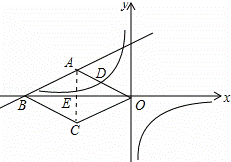
如图,在平面直角坐标系中,四边形ABCD是菱形,B、O在x轴负半轴上,AO=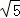 ,tan∠AOB=
,tan∠AOB=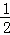 ,一次函数y=k1x+b的图象过A、B两点,反比例函数y=
,一次函数y=k1x+b的图象过A、B两点,反比例函数y=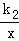 的图象过OA的中点D.
的图象过OA的中点D.
(1)求一次函数和反比例函数的表达式;
(2)平移一次函数y=k1x+b的图象,当一次函数y=k1x+b的图象与反比例函数y=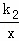 的图象无交点时,求b的取值范围.
的图象无交点时,求b的取值范围.

解:(1)连接AC,交OB于E,如图所示:
∵四边形ABCO是菱形,
∴BE=OE=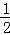 OB,OB⊥AC,
OB,OB⊥AC,
∴∠AEO=90°,
∴tan∠AOB=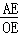 =
=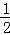 ,
,
∴OE=2AE,
设AE=x,则OE=2x,
根据勾股定理得:OA=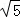 x=
x=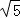 ,
,
∴x=1,
∴AE=1,OE=2,
∴OB=2OE=4,
∴A(﹣2,1),B(﹣4,0),
把点A(﹣2,1),B(﹣4,0)代入一次函数y=k1x+b得: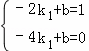 ,
,
解得:k1=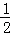 ,b=2,
,b=2,
∴一次函数的解析式为:y=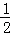 x+2;
x+2;
∵D是OA的中点,A(﹣2,1),
∴D(﹣1,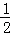 ),
),
把点D(﹣1,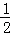 )代入反比例函数y=
)代入反比例函数y=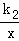 得:k2=﹣
得:k2=﹣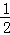 ,
,
∴反比例函数的解析式为:y=﹣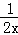 ;
;
(2)根据题意得:一次函数的解析式为:y=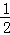 x+b,
x+b,
∵一次函数y=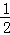 x+b的图象与反比例函数y=﹣
x+b的图象与反比例函数y=﹣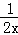 的图象无交点,
的图象无交点,
∴方程组 无解,
无解,
即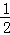 x+b=﹣
x+b=﹣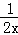 无解,
无解,
整理得:x2+2bx+1=0,
∴△=(2b)2﹣4×1×1<0,b2<1,
解得:﹣1<b<1,
∴当一次函数y=k1x+b的图象与反比例函数y=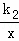 的图象无交点时,b的取值范围是﹣1<b<1.
的图象无交点时,b的取值范围是﹣1<b<1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的值为0,则x的值为 .
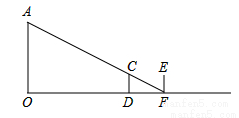
的值为0,则x的值为 . 点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:EC,⑤OD2=DE•CD,正确的有( )
点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:EC,⑤OD2=DE•CD,正确的有( )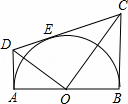
 ﹣
﹣ |
|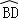 ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )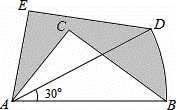
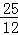 π B.
π B. 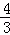 π C.
π C. 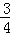 π D.
π D.  π
π