��Ŀ����
��֪������y=x2+bx+c����A��﹣1��0����B��3��0�����㣬��y���ཻ�ڵ�C���������ߵĶ���Ϊ��D��
��1����������ߵĽ���ʽ����D�����ꣻ
��2������AC��CD��BD��BC�����AOC����BOC����BCD������ֱ�ΪS1��S2��S3���õ�ʽ��ʾS1��S2��S3֮���������ϵ����˵�����ɣ�
��3����M���߶�AB��һ���㣨��������A�͵�B��������M��MN��BC��AC�ڵ�N������MC���Ƿ���ڵ�Mʹ��AMN=��ACM�������ڣ������M������ʹ�ʱ��ֱ��MN�Ľ���ʽ���������ڣ���˵�����ɣ�
�⣺��1����������y=x2+bx+c����A��﹣1��0����B��3��0�����㣬
�� ��
��
��� ��
��
�������ߵĽ���ʽΪ��y=x2﹣2x﹣3��
y=x2﹣2x﹣3=��x﹣1��2﹣4��
���D������Ϊ����1��﹣4����
��2��S1+S3=S2��
����D��DE��x���ڵ�E��DF��y����F��
������ã�CD= ��BD=2
��BD=2 ��BC=3
��BC=3 ��
��
CD2+BC2=BD2��
���BCD��ֱ�������Σ�
S1= ��OA��OC=
��OA��OC= ��
��
S2= ��OB��OC=
��OB��OC=
S3��= ��CD��BC=3��
��CD��BC=3��
��S1+S3=S2��
��3�����ڵ�Mʹ��AMN=��ACM��
���M��������m��0����
��﹣1��m��3��
��MA=m+1��AC= ��
��
��MN��BC��
�� =
= ����
���� =
= ��
��
��ã�AN= ��m+1����
��m+1����
�ߡ�AMN=��ACM����MAN=��CAM��
���AMN�ס�ACM��
�� =
= ������m+1��2=
������m+1��2= •
• ��m+1����
��m+1����
��ã�m1= ��m2=﹣1����ȥ����
��m2=﹣1����ȥ����
���M�������� ��0����
��0����
��BC�Ľ���ʽΪ y=kx+b����B��3��0����C��0��﹣3������ã�
y=kx+b����B��3��0����C��0��﹣3������ã�
 �����
����� ��
��
��BC�Ľ���ʽΪy=x﹣3����MN��BC��
����ֱ��MN�Ľ���ʽΪy=x+b���ѵ�M������Ϊ�� ��0������ã�
��0������ã�
b=﹣ ��
��
��ֱ��MN�Ľ���ʽΪy=x﹣ ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�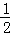 x��kx+b��﹣2�Ľ⼯Ϊ��������
x��kx+b��﹣2�Ľ⼯Ϊ��������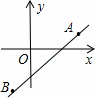
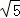 ��tan��AOB=
��tan��AOB=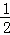 ��һ�κ���y=k1x+b��ͼ���A��B���㣬����������y=
��һ�κ���y=k1x+b��ͼ���A��B���㣬����������y=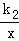 ��ͼ���OA���е�D��
��ͼ���OA���е�D��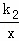 ��ͼ������ʱ����b��ȡֵ��Χ��
��ͼ������ʱ����b��ȡֵ��Χ��
 ����
���� =������
=������
 �Ľ⼯��__________.
�Ľ⼯��__________. 
 .
.