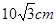题目内容
如图,直角梯形ABCD中,AD∥BC,∠A=90°, ,
, 交AB于E,DF平分∠EDC交BC于F,连结EF.
交AB于E,DF平分∠EDC交BC于F,连结EF.

(1)证明: ;
;
(2)若 ,求CF的长.
,求CF的长.
 ,
, 交AB于E,DF平分∠EDC交BC于F,连结EF.
交AB于E,DF平分∠EDC交BC于F,连结EF.
(1)证明:
 ;
;(2)若
 ,求CF的长.
,求CF的长.(1)证明见解析(2)5
(1)证明:过D作DG⊥BC于G.
由已知可得,四边形ABGD为正方形. …………1分
∵DE⊥DC,
∴∠ADE+∠EDG=90°=∠GDC+∠EDG,
∴∠ADE=∠GDC. ………………………3分
又∵∠A=∠DGC,且AD=GD,
∴△ADE≌△GDC.
∴DE=DC,且AE=GC. ……………………4分
在△EDF和△CDF中,
∠EDF=∠CDF,DE=DC,DF为公共边,
∴△EDF≌△CDF.
∴EF=CF. ……………………………………………6分
(2)∵AD=3AE, ∴ . ………………………………………7分
. ………………………………………7分
设 ,则
,则 ,BE=6-2="4."
,BE=6-2="4."
由勾股定理,得 .
.
解之,得 , 即
, 即 .
.
∴CF = EF=5……………………………10分
(1)过D作DG⊥BC于G,由已知可得四边形ABGD为正方形,然后利用正方形的性质和已知条件证明△ADE≌△GDC,接着利用全等三角形的性质证明△EDF≌△CDF,
(2)由(1)得 ,设
,设 ,利用勾股定理求解
,利用勾股定理求解
由已知可得,四边形ABGD为正方形. …………1分
∵DE⊥DC,
∴∠ADE+∠EDG=90°=∠GDC+∠EDG,
∴∠ADE=∠GDC. ………………………3分
又∵∠A=∠DGC,且AD=GD,
∴△ADE≌△GDC.
∴DE=DC,且AE=GC. ……………………4分
在△EDF和△CDF中,
∠EDF=∠CDF,DE=DC,DF为公共边,
∴△EDF≌△CDF.
∴EF=CF. ……………………………………………6分
(2)∵AD=3AE, ∴
 . ………………………………………7分
. ………………………………………7分设
 ,则
,则 ,BE=6-2="4."
,BE=6-2="4." 由勾股定理,得
 .
. 解之,得
 , 即
, 即 .
. ∴CF = EF=5……………………………10分
(1)过D作DG⊥BC于G,由已知可得四边形ABGD为正方形,然后利用正方形的性质和已知条件证明△ADE≌△GDC,接着利用全等三角形的性质证明△EDF≌△CDF,
(2)由(1)得
 ,设
,设 ,利用勾股定理求解
,利用勾股定理求解 
练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
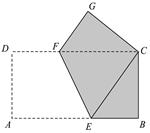

 中,
中, ∥
∥ ,
, ,
, ,
, ,
, ,将
,将 平移到
平移到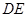 处。
处。
 是直角三角形吗?请说明理由;
是直角三角形吗?请说明理由; 上的高;
上的高; 90°,BD⊥DC,BD=DC,CE平分
90°,BD⊥DC,BD=DC,CE平分 ,交AB于点E,交BD于点H,EN∥DC交BD于点N,下列结论:①BH=DH;②
,交AB于点E,交BD于点H,EN∥DC交BD于点N,下列结论:①BH=DH;②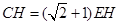 ;③
;③ ,其中正确的是( )
,其中正确的是( )