题目内容
13.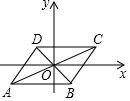 如图,已知?ABCD的顶点A在第三象限,顶点B在第四象限,对角线AC的中点在坐标原点,一边AB与x轴平行且AB=2,若点A的坐标为(a,b),则点D的坐标为(-a-2,-b).
如图,已知?ABCD的顶点A在第三象限,顶点B在第四象限,对角线AC的中点在坐标原点,一边AB与x轴平行且AB=2,若点A的坐标为(a,b),则点D的坐标为(-a-2,-b).
分析 根据平行四边形的性质得到CD=AB=2,根据已知条件得到B(2+a,b),由于点D与点B关于原点对称,即可得到结论.
解答 解:∵AB与x轴平行且AB=2,A(a,b),
∴B(a+2,b),
∵对角线AC的中点在坐标原点,
∴点A、C关于原点对称,
∵四边形ABCD为平行四边形,
∴点B、D关于原点对称,
∴D(-a-2,-b);
故答案为:(-a-2,-b).
点评 本题考查了平行四边形的性质,坐标与图形的性质,关于原点对称的点的坐标特征,熟练掌握平行四边形的性质是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.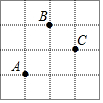 在如图的方格纸上,若用(-1,1)表示A点,(0,3)表示B点,那么C点的位置可表示为( )
在如图的方格纸上,若用(-1,1)表示A点,(0,3)表示B点,那么C点的位置可表示为( )
 在如图的方格纸上,若用(-1,1)表示A点,(0,3)表示B点,那么C点的位置可表示为( )
在如图的方格纸上,若用(-1,1)表示A点,(0,3)表示B点,那么C点的位置可表示为( )| A. | (1,2) | B. | (2,3) | C. | (3,2) | D. | (2,1) |
18.下列各组数据中的三个数,可作为三边长构成直角三角形的是( )
| A. | 4,5,6 | B. | 2,3,4 | C. | 11,12,13 | D. | 8,15,17 |
5. 如图,菱形ABCD的周长为32cm,对角线AC、BD相交于点O,E是AD的中点,连接OE,则线段OE的长等于( )
如图,菱形ABCD的周长为32cm,对角线AC、BD相交于点O,E是AD的中点,连接OE,则线段OE的长等于( )
 如图,菱形ABCD的周长为32cm,对角线AC、BD相交于点O,E是AD的中点,连接OE,则线段OE的长等于( )
如图,菱形ABCD的周长为32cm,对角线AC、BD相交于点O,E是AD的中点,连接OE,则线段OE的长等于( )| A. | 3cm | B. | 3.5cm | C. | 4cm | D. | 5cm |
3.下列调查中,适合采用全面调查方式的是( )
| A. | 对我县某学校某班50名同学体重情况的调查 | |
| B. | 对我县幸福河水质情况的调查 | |
| C. | 对我县某类烟花爆竹燃放安全情况的调查 | |
| D. | 对我县端午节期间市场上粽子质量情况的调查 |
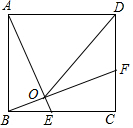 如图,在正方形ABCD中,AB=5.点E为BC边上一点(不与点B重合),点F为CD边上一点,线段AE、BF相交于点O,其中AE=BF.
如图,在正方形ABCD中,AB=5.点E为BC边上一点(不与点B重合),点F为CD边上一点,线段AE、BF相交于点O,其中AE=BF.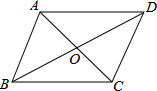 如图,?ABCD的对角线AC、BD相交于点O,则添加一个适当的条件:AC=BD(答案不唯一),可使其成为矩形(只填一个即可).
如图,?ABCD的对角线AC、BD相交于点O,则添加一个适当的条件:AC=BD(答案不唯一),可使其成为矩形(只填一个即可).