题目内容
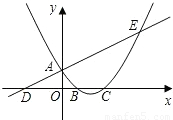
(2009•眉山)如图,已知直线y= x+1与y轴交于点A,与x轴交于点D,抛物线y=
x+1与y轴交于点A,与x轴交于点D,抛物线y= x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).(1)求该抛物线的解析式;
(2)动点P在x轴上移动,当△PAE是直角三角形时,求点P的坐标P;
(3)在抛物线的对称轴上找一点M,使|AM-MC|的值最大,求出点M的坐标.

【答案】分析:(1)易得点A(0,1),那么把A,B坐标代入y= x2+bx+c即可求得函数解析式;
x2+bx+c即可求得函数解析式;
(2)让直线解析式与抛物线的解析式结合即可求得点E的坐标.△PAE是直角三角形,应分点P为直角顶点,点A是直角顶点,点E是直角顶点三种情况探讨;
(3)易得|AM-MC|的值最大,应找到C关于对称轴的对称点B,连接AB交对称轴的一点就是M.应让过AB的直线解析式和对称轴的解析式联立即可求得点M坐标.
解答: 解:(1)将A(0,1)、B(1,0)坐标代入y=
解:(1)将A(0,1)、B(1,0)坐标代入y= x2+bx+c
x2+bx+c
得 ,
,
解得 ,
,
∴抛物线的解折式为y= x2-
x2- x+1;(2分)
x+1;(2分)
(2)设点E的横坐标为m,则它的纵坐标为 m2-
m2- m+1,
m+1,
即E点的坐标(m, m2-
m2- m+1),
m+1),
又∵点E在直线y= x+1上,
x+1上,
∴ m2-
m2- m+1=
m+1= m+1
m+1
解得m1=0(舍去),m2=4,
∴E的坐标为(4,3).(4分)
(Ⅰ)当A为直角顶点时,
过A作AP1⊥DE交x轴于P1点,设P1(a,0)易知D点坐标为(-2,0),
由Rt△AOD∽Rt△P1OA得
 即
即 ,
,
∴a= ,
,
∴P1( ,0).(5分)
,0).(5分)
(Ⅱ)同理,当E为直角顶点时,过E作EP2⊥DE交x轴于P2点,
由Rt△AOD∽Rt△P2ED得,
 即
即 =
= ,
,
∴EP2= ,
,
∴DP2= =
=
∴a= -2=
-2= ,
,
P2点坐标为( ,0).(6分)
,0).(6分)
(Ⅲ)当P为直角顶点时,过E作EF⊥x轴于F,设P3(b、0),
由∠OPA+∠FPE=90°,得∠OPA=∠FEP,Rt△AOP∽Rt△PFE,
由 得
得 ,
,
解得b1=3,b2=1,
∴此时的点P3的坐标为(1,0)或(3,0),(8分)
综上所述,满足条件的点P的坐标为( ,0)或(1,0)或(3,0)或(
,0)或(1,0)或(3,0)或( ,0);
,0);
(3)抛物线的对称轴为 ,(9分)
,(9分)
∵B、C关于x= 对称,
对称,
∴MC=MB,
要使|AM-MC|最大,即是使|AM-MB|最大,
由三角形两边之差小于第三边得,当A、B、M在同一直线上时|AM-MB|的值最大.(10分)
易知直线AB的解折式为y=-x+1
∴由 ,
,
得 ,
,
∴M( ,-
,- ).(11分)
).(11分)
点评:一个三角形是直角三角形,应分不同顶点为直角等多种情况进行分析;
求两条线段和或差的最值,都要考虑做其中一点关于所求的点在的直线的对称点.
 x2+bx+c即可求得函数解析式;
x2+bx+c即可求得函数解析式;(2)让直线解析式与抛物线的解析式结合即可求得点E的坐标.△PAE是直角三角形,应分点P为直角顶点,点A是直角顶点,点E是直角顶点三种情况探讨;
(3)易得|AM-MC|的值最大,应找到C关于对称轴的对称点B,连接AB交对称轴的一点就是M.应让过AB的直线解析式和对称轴的解析式联立即可求得点M坐标.
解答:
 解:(1)将A(0,1)、B(1,0)坐标代入y=
解:(1)将A(0,1)、B(1,0)坐标代入y= x2+bx+c
x2+bx+c得
 ,
,解得
 ,
,∴抛物线的解折式为y=
 x2-
x2- x+1;(2分)
x+1;(2分)(2)设点E的横坐标为m,则它的纵坐标为
 m2-
m2- m+1,
m+1,即E点的坐标(m,
 m2-
m2- m+1),
m+1),又∵点E在直线y=
 x+1上,
x+1上,∴
 m2-
m2- m+1=
m+1= m+1
m+1解得m1=0(舍去),m2=4,
∴E的坐标为(4,3).(4分)
(Ⅰ)当A为直角顶点时,
过A作AP1⊥DE交x轴于P1点,设P1(a,0)易知D点坐标为(-2,0),
由Rt△AOD∽Rt△P1OA得
 即
即 ,
,∴a=
 ,
,∴P1(
 ,0).(5分)
,0).(5分)(Ⅱ)同理,当E为直角顶点时,过E作EP2⊥DE交x轴于P2点,
由Rt△AOD∽Rt△P2ED得,
 即
即 =
= ,
,∴EP2=
 ,
,∴DP2=
 =
=
∴a=
 -2=
-2= ,
,P2点坐标为(
 ,0).(6分)
,0).(6分)(Ⅲ)当P为直角顶点时,过E作EF⊥x轴于F,设P3(b、0),
由∠OPA+∠FPE=90°,得∠OPA=∠FEP,Rt△AOP∽Rt△PFE,
由
 得
得 ,
,解得b1=3,b2=1,
∴此时的点P3的坐标为(1,0)或(3,0),(8分)
综上所述,满足条件的点P的坐标为(
 ,0)或(1,0)或(3,0)或(
,0)或(1,0)或(3,0)或( ,0);
,0);(3)抛物线的对称轴为
 ,(9分)
,(9分)∵B、C关于x=
 对称,
对称,∴MC=MB,
要使|AM-MC|最大,即是使|AM-MB|最大,
由三角形两边之差小于第三边得,当A、B、M在同一直线上时|AM-MB|的值最大.(10分)
易知直线AB的解折式为y=-x+1
∴由
 ,
,得
 ,
,∴M(
 ,-
,- ).(11分)
).(11分)点评:一个三角形是直角三角形,应分不同顶点为直角等多种情况进行分析;
求两条线段和或差的最值,都要考虑做其中一点关于所求的点在的直线的对称点.

练习册系列答案
相关题目
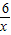 上,且OA=4,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B,则△ABC的周长为( )
上,且OA=4,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B,则△ABC的周长为( )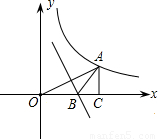
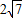
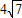
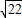
 x+1与y轴交于点A,与x轴交于点D,抛物线y=
x+1与y轴交于点A,与x轴交于点D,抛物线y= x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).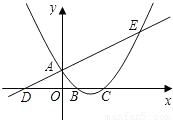
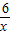 上,且OA=4,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B,则△ABC的周长为( )
上,且OA=4,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B,则△ABC的周长为( )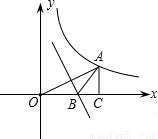
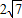
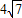
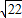
 x+1与y轴交于点A,与x轴交于点D,抛物线y=
x+1与y轴交于点A,与x轴交于点D,抛物线y= x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).