题目内容
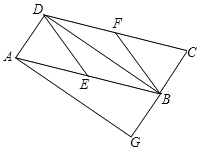
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,
上一点,![]() ,
,![]() ,垂足为
,垂足为![]() ,
,![]() 交
交![]() 于
于![]() .若
.若![]() ,试求
,试求![]() 的值.
的值.
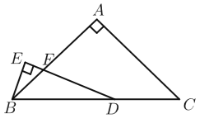
【答案】![]()
【解析】
由AB=AC,∠A=90![]() 可得出∠C=45
可得出∠C=45![]() ,过点D作DH∥AC,交AB于点H,交BE的延长线于点G,则∠BDH=∠C=45
,过点D作DH∥AC,交AB于点H,交BE的延长线于点G,则∠BDH=∠C=45![]() ,∠BHD=∠A=90
,∠BHD=∠A=90![]() ,进而可得出△HBD为等腰直角三角形,根据等腰直角三角形的性质可得出HB=HD,由∠BDE=
,进而可得出△HBD为等腰直角三角形,根据等腰直角三角形的性质可得出HB=HD,由∠BDE=![]() ∠C可得出∠BDE=
∠C可得出∠BDE=![]() ∠BCH,及DE平分∠BDG,结合DE⊥BG可得出BE=
∠BCH,及DE平分∠BDG,结合DE⊥BG可得出BE=![]() BG,由等角的余角相等可得出∠DFH=∠G,∠GBH=∠FDH,再结合BH=DH即可证出△BGH≌△DFH(AAS),利用全等三角形的性质可证出BG=DF,结合BE=
BG,由等角的余角相等可得出∠DFH=∠G,∠GBH=∠FDH,再结合BH=DH即可证出△BGH≌△DFH(AAS),利用全等三角形的性质可证出BG=DF,结合BE=![]() BG可得出BE=
BG可得出BE=![]() FD,即可求解.
FD,即可求解.
过点D作DH∥AC,交AB于点H,交BE的延长线于点G,如图,

∵AB=AC,∠A=90![]() ,
,
∴∠C=45![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
而![]() ,
,
∵![]() ,
,
∴![]() 平分
平分![]() ,
,
而![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]()
在![]() 和
和![]() 中
中
 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.

练习册系列答案
相关题目