Question

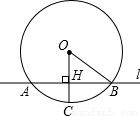
如图，直线l与⊙O相交于A，B两点，且与半径OC垂直，垂足为H，已知AB=16cm，．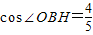
（1）求⊙O的半径；
（2）如果要将直线l向下平移到与⊙O相切的位置，平移的距离应是多少？请说明理由．

Answer 1

【答案】分析：（1）Rt△OHB中，由垂径定理易得BH的长，可利用∠OBH的余弦函数求出半径OB的长；
（2）由切线的性质知，若直线l与⊙O相切，那么直线l必过C点，故所求的平移距离应该是线段CH的长．
Rt△OHB中，根据勾股定理，可求出OH的长．CH=OC-OH．
解答：解：（1）∵直线l与半径OC垂直，
∴HB=AB==8（cm）．                      （2分）
∵cos∠OBH==，
∴OB=HB=×8=10（cm）；（2分）

（2）在Rt△OBH中，
OH===6（cm）．           （2分）
∴CH=10-6=4（cm）．
所以将直线l向下平移到与⊙O相切的位置时，平移的距离是4cm．（2分）
点评：此题综合考查了垂径定理、切线的性质及解直角三角形的应用．