题目内容
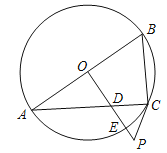
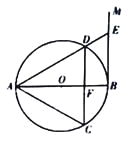
【题目】在等腰直角三角形ABC中,∠BAC=90°,AB=AC=2,直角三角板含45°角的顶点P在边BC上移动(点P不与B,C重合),如图,直角三角板的一条直角边始终经过点A,斜边与边AC交于点Q,当△ABP为等腰三角形时,CQ的长为_____.

【答案】1或2![]() ﹣2.
﹣2.
【解析】
由等腰直角三角形的性质得BC![]() AB=2
AB=2![]() ,∠B=∠C=45°,再证明∠BAP=∠CPQ,则可判断△CPQ∽△BAP,所以
,∠B=∠C=45°,再证明∠BAP=∠CPQ,则可判断△CPQ∽△BAP,所以![]() ,分两种情况讨论:当PB=PA时,易得AP⊥BC,BP=CP
,分两种情况讨论:当PB=PA时,易得AP⊥BC,BP=CP![]() BC
BC![]() ,利用相似比可计算出CQ=1;当BP=AB=2时,易得PC=2
,利用相似比可计算出CQ=1;当BP=AB=2时,易得PC=2![]() 2,利用相似比可计算出此时CQ=2
2,利用相似比可计算出此时CQ=2![]() 2.
2.
∵△ABC为等腰直角三角形,∴BC![]() AB=2
AB=2![]() ,∠B=∠C=45°.
,∠B=∠C=45°.
∵∠APC=∠B+∠BAP,即∠APQ+∠CPQ=∠B+∠BAP,而∠APQ=45°,∴∠BAP=∠CPQ,∴△CPQ∽△BAP,∴![]() .分两种情况讨论:
.分两种情况讨论:
当PB=PA时,则AP⊥BC,此时BP=CP![]() BC
BC![]() ,∴CQ
,∴CQ![]() 1;
1;
当BP=AB=2时,此时PC=2![]() 2,∴CQ
2,∴CQ![]() 2.
2.
综上所述:CQ的长为1或2![]() 2.
2.
故答案为:1或2![]() 2.
2.

 口算能手系列答案
口算能手系列答案【题目】在一个不透明的袋子中装有红、黄两种颜色的球共20个,每个球除颜色外完全相同.某学习兴趣小组做摸球实验,将球搅匀后从中随机摸出1个球,记下颜色后再放回袋中,不断重复.下表是活动进行中的部分统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到红球的次数m | 59 | 96 | 118 | 290 | 480 | 601 |
摸到红球的频率 | 0.59 | 0.58 | 0.60 | 0.601 |
(1)完成上表;
(2)“摸到红球”的概率的估计值 (精确到0.1)
(3)试估算袋子中红球的个数.
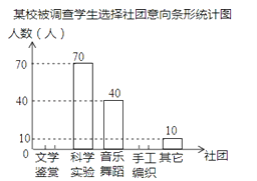
【题目】为了深化改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
某校被调查学生选择社团意向统计表
选择意向 | 所占百分比 |
文学鉴赏 | a |
科学实验 | 35% |
音乐舞蹈 | b |
手工编织 | 10% |
其他 | c |
根据统计图表中的信息,解答下列问题:
(1)求本次调查的学生总人数及a,b,c的值;
(2)将条形统计图补充完整;
(3)若该校共有1200名学生,试估计全校选择“科学实验”社团的人数.