题目内容
18．给出下列函数：①y=-6x；②y=-$\frac{6}{x}$x；③y=6x2；④y=8x+1．其中一次函数有（ ）| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
分析 逐一分析四个函数是否为一次函数，由此即可得出结论．
解答 解：①y=-6x是一次函数；
②y=-$\frac{6}{x}$x=-6（x≠0）为常数函数，不是一次函数；
③y=6x2为二次函数，不是一次函数；
④y=8x+1为一次函数．
故选C．
点评 本题考查了一次函数的定义，根据一次函数的定义逐一分析四个函数是否为一次函数是解题的关键．
练习册系列答案
相关题目
8．△ABC中，直线DE交AB于点D，交AC于点E，以下能推出DE∥BC的条件是（ ）
| A． | $\frac{AD}{AB}$=$\frac{3}{4}$，$\frac{AE}{EC}$=$\frac{3}{4}$ | B． | $\frac{AD}{AB}$=$\frac{3}{4}$，$\frac{DE}{BC}$=$\frac{3}{4}$ | C． | $\frac{AD}{DB}$=$\frac{2}{3}$，$\frac{CE}{EA}$=$\frac{2}{3}$ | D． | $\frac{AB}{AD}$=$\frac{4}{3}$，$\frac{EC}{AE}$=$\frac{1}{3}$ |
9．
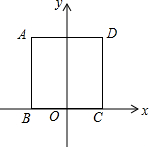正方形ABCD在直角坐标系中如图放置，B点的坐标是（-2，0），C点的坐标是（2，0），则A点的坐标是（ ）
正方形ABCD在直角坐标系中如图放置，B点的坐标是（-2，0），C点的坐标是（2，0），则A点的坐标是（ ）| A． | （4，-2） | B． | （-2，1） | C． | （2，4） | D． | （-2，4） |
13．给定一列按规律排列的数：$\frac{1}{2}$，$\frac{2}{5}$，$\frac{3}{10}$，$\frac{4}{17}$，…，则这列数的第6个数是（ ）
| A． | $\frac{6}{35}$ | B． | $\frac{5}{26}$ | C． | $\frac{6}{37}$ | D． | $\frac{7}{39}$ |
10．下列各式变形正确的是（ ）
| A． | $\frac{2}{2+a}=\frac{1}{1+a}$ | B． | $\frac{1}{x+1}=\frac{x-1}{{{x^2}-1}}$ | C． | $\frac{-x+y}{x-y}=\frac{x+y}{y-x}$ | D． | $\frac{{{a^2}-1}}{a+1}=a-1$ |