题目内容
在边长为a的正方形中挖去一个边长为b的小正方形（a＞b）（如图甲），把余下的部分拼成一个矩形（如图乙），根据两个图形中阴影部分的面积相等，可以验证
- A.（a+b）2=a2+2ab+b2
- B.（a-b）2=a2-2ab+b2
- C.a2-b2=（a+b）（a-b）
- D.（a+2b）（a-b）=a2+ab-2b2
C
分析：利用正方形的面积公式可知：阴影部分的面积=a2-b2=（a+b）（a-b）．
解答：阴影部分的面积=a2-b2=（a+b）（a-b）．
故选C．
点评：此题主要考查了乘法的平方差公式．即两个数的和与这两个数的差的积等于这两个数的平方差，这个公式就叫做平方差公式．
分析：利用正方形的面积公式可知：阴影部分的面积=a2-b2=（a+b）（a-b）．
解答：阴影部分的面积=a2-b2=（a+b）（a-b）．
故选C．
点评：此题主要考查了乘法的平方差公式．即两个数的和与这两个数的差的积等于这两个数的平方差，这个公式就叫做平方差公式．
练习册系列答案
相关题目
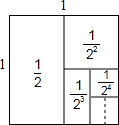在数学兴趣小组活动中，小明为了求
如图，在边长为1的正方形中，以各顶点为圆心，对角线的一半为半径在正方形内作弧，则图中阴影部分的面积是
（如图2），利用这两幅图形面积，可以验证的公式是（ ）