题目内容
如图，OB、OC、OD是∠AOE内的三条射线，问图中有____个角．
- A.8个
- B.9个
- C.10个
- D.11个
C
分析：过O点的每两条射线都能构成一个角，可据此判定角的个数．
解答：射线OA可与其它4条射线组成4个角，则5条射线一共有4×5=20个角；
由于每两条组成一个角，故图中角的个数为20÷2=10个．
故选C．
点评：此题主要考查的是角的定义：具有公共点的两条射线组成的图形叫做角．
分析：过O点的每两条射线都能构成一个角，可据此判定角的个数．
解答：射线OA可与其它4条射线组成4个角，则5条射线一共有4×5=20个角；
由于每两条组成一个角，故图中角的个数为20÷2=10个．
故选C．
点评：此题主要考查的是角的定义：具有公共点的两条射线组成的图形叫做角．
练习册系列答案
相关题目
16、如图，OB，OC是∠AOD的任意两条射线，OM平分∠AOB，ON平分∠COD，若∠MON=α，∠BOC=β，则表示∠AOD的代数式是∠AOD=
如图，OB、OC分别为∠ABC，∠ACB的平分线，∠BOC随着∠A的变化而变化．为探究∠A和∠BOC的关系，现采取如下两种方案，在变化过程中，设∠A为x°，∠BOC为y°．
方案甲：用量角器量出∠A、∠BOC的不断变化时的具体数据，并列表如下：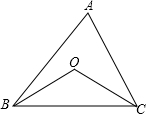
建立直角坐标系，并描点、连线，猜测y与x之间的函数关系，求出y与x的函数关系式．
方案乙：利用角平分线的性质及三角形内角和为180°的性质，直接进行计算，求出y与x之间的函数关系．
（1）若x=60°，则y= ．（请直接写
出结果）
（2）请采用方案甲或方案乙中的一种进行解答，得到∠A与∠BOC之间的关系．
方案甲：用量角器量出∠A、∠BOC的不断变化时的具体数据，并列表如下：
| x | 10 | 20 | 30 | 40 | … |
| y | 95 | 100 | 105 | 110 | … |
方案乙：利用角平分线的性质及三角形内角和为180°的性质，直接进行计算，求出y与x之间的函数关系．
（1）若x=60°，则y=
出结果）（2）请采用方案甲或方案乙中的一种进行解答，得到∠A与∠BOC之间的关系．
19、如图，OB、OC是⊙O的半径，A是⊙O上一点，若已知∠B=20°，∠C=30°，则∠A=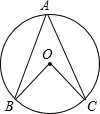
如图，OB、OC是⊙O的半径，A是⊙O上一点，若∠B=20°，∠C=30°，则∠BOC=
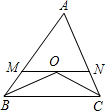如图，OB、OC分别平分∠ABC与∠ACB，MN∥BC，若AB=24，AC=36，则△AMN的周长是