题目内容
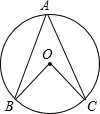如图，OB、OC是⊙O的半径，A是⊙O上一点，若∠B=20°，∠C=30°，则∠BOC=100°
100°
．分析：连结OA，利用等腰三角形的性质易得∠OAB=∠B=20°，∠OAC=∠C=30°，则∠BAC=50°，然后根据圆周角定理即可得到∠BOC=2∠BAC=100°．
解答：
解：连结OA，如图，
∵OA=OB，OA=OC，
∴∠OAB=∠B=20°，∠OAC=∠C=30°，
∴∠BAC=∠OAB+∠OAC=50°，
∴∠BOC=2∠BAC=100°．
故答案为100°．
解：连结OA，如图，∵OA=OB，OA=OC，
∴∠OAB=∠B=20°，∠OAC=∠C=30°，
∴∠BAC=∠OAB+∠OAC=50°，
∴∠BOC=2∠BAC=100°．
故答案为100°．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
相关题目
16、如图，OB，OC是∠AOD的任意两条射线，OM平分∠AOB，ON平分∠COD，若∠MON=α，∠BOC=β，则表示∠AOD的代数式是∠AOD=
10、如图，OB、OC是∠ABC、∠ACB的角平分线，∠BOC=140°，则∠A等于（ ）
19、如图，OB、OC是⊙O的半径，A是⊙O上一点，若已知∠B=20°，∠C=30°，则∠A=
如图，OB、OC是⊙O的半径，A是⊙O上一点，若∠BOC=100°，则∠BAC等于（ ）
如图，OB，OC是⊙O的半径，已知∠B=20°，∠C=30°，则∠BOC=（ ）