题目内容
若2x|2a+1|y与
xy|b|是同类项，其中a，b互为倒数，求2（a-2b2）-（3b2-a）的值．
解：根据题意，得
，
又∵a，b互为倒数，∴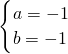
，
∴原式=2（a-2b2）-（3b2-a）=2（-1-2）-（3+1）=-8．
分析：根据倒数的定义可得ab=1，根据同类项的概念可得方程：|2a+1|=1，|b|=1，解方程求得a，b的值，从而求出代数式的值．
点评：主要考查倒数的概念及性质．倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数．
，又∵a，b互为倒数，∴
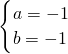，∴原式=2（a-2b2）-
（3b2-a）=2（-1-2）-（3+1）=-8．分析：根据倒数的定义可得ab=1，根据同类项的概念可得方程：|2a+1|=1，|b|=1，解方程求得a，b的值，从而求出代数式的值．
点评：主要考查倒数的概念及性质．倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数．
练习册系列答案
相关题目
xy|b|是同类项，其中a，b互为倒数，求2（a﹣2b2）﹣
（3b2﹣a）的值。