题目内容
 如图,矩形ABCD,E、F、G、H分别为AD、AB、BC、CD的中点,求证:四边形EFGH为菱形.
如图,矩形ABCD,E、F、G、H分别为AD、AB、BC、CD的中点,求证:四边形EFGH为菱形.考点:中点四边形
专题:证明题
分析:根据矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,利用三角形中位线定理求证EF=GH=FG=EH,然后利用四条边都相等的平行四边形是菱形即可判定.
解答: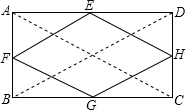 证明:连接BD,AC.
证明:连接BD,AC.
∵矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,
∴AC=BD,
∵EF为△ABD的中位线,
∴EF=
BD,EF∥BD,
又GH为△BCD的中位线,
∴GH=
BD,GH∥BD,
同理FG为△ABC的中位线,
∴FG=
AC,FG∥AC,
EH为△ACD的中位线,
∴EH=
AC,EH∥AC,
∴EF=GH=FG=EH,
∴四边形EFGH是菱形.
 证明:连接BD,AC.
证明:连接BD,AC.∵矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,
∴AC=BD,
∵EF为△ABD的中位线,
∴EF=
| 1 |
| 2 |
又GH为△BCD的中位线,
∴GH=
| 1 |
| 2 |
同理FG为△ABC的中位线,
∴FG=
| 1 |
| 2 |
EH为△ACD的中位线,
∴EH=
| 1 |
| 2 |
∴EF=GH=FG=EH,
∴四边形EFGH是菱形.
点评:此题主要考查学生对菱形的判定、三角形中位线定理、和矩形的性质的理解和掌握,证明此题的关键是利用三角形中位线定理求证EF=
BD,EF∥BD,GH=
BD,GH∥BD,FG=
AC,FG∥AC,EH=
AC,EH∥AC.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目
已知点P(a+b,ab),其中a<0,b<0;则点P在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
两列数如下:
7,10,13,16,19,22,25,28,31,…
7,11,15,19,23,27,31,35,39,…
第1个相同的数是7,第10个相同的数是( )
7,10,13,16,19,22,25,28,31,…
7,11,15,19,23,27,31,35,39,…
第1个相同的数是7,第10个相同的数是( )
| A、115 | B、127 |
| C、139 | D、151 |
 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一条线段AB,点A、B均与小正方形的顶点重合.
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一条线段AB,点A、B均与小正方形的顶点重合. 如图,已知∠1=34°40′,OD平分∠BOC,求∠AOD的度数.
如图,已知∠1=34°40′,OD平分∠BOC,求∠AOD的度数.
 如图,已知锐角△ABC的面积为1,正方形DEFG是△ABC的一个内接三角形,DG∥BC,求正方形DEFG面积的最大值.
如图,已知锐角△ABC的面积为1,正方形DEFG是△ABC的一个内接三角形,DG∥BC,求正方形DEFG面积的最大值.