题目内容
已知：关于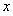
的方程x2+(2-m)x-2m=0.
⑴求证：无论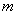
取什么实数值，方程总有实数根；
⑵取一个m的值，使得方程两根均为整数，并求出方程的两根。
【答案】
（1）证明见解析；（2）0（答案不唯一）.
【解析】
试题分析：（1）只要看根的判别式△=b2-4ac的值的符号就可以了；
（2）m可取比较简单的数，如0或1等，并通过解方程判断方程的根是否是整数．
试题解析: （1）△=（2-m）2-4×2m=（m-2）2≥0，所以方程总有实数根；
（2）当m=0时，原方程化为：x2+2x=0，
x（x+2）=0，
解得x=0或-2．
考点: 1.解一元二次方程-因式分解法；2.根的判别式．
练习册系列答案
阅读快车系列答案
相关题目