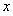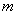题目内容
已知：关于的方程x2-kx-2=0．（1）求证：无论k为何值时，方程有两个不相等的实数根．
（2）设方程的两根为x1，x2，若2（x1+x2）＞x1x2，求k的取值范围．
【答案】分析：（1）根据根的判别式△=b2-4ac来确定方程的根的情况；
（2）由根与系数的关系x1+x2=-
、x1x2=
来求k的取值范围．
解答：解：（1）证明：由方程x2-kx-2=0知
a=1，b=-k，c=-2，
∴△=b2-4ac
=（-k）2-4×1×（-2）
=k2+8＞0，
∴无论k为何值时，方程有两个不相等的实数根；
（2）∵方程x2-kx-2=0．的两根为x1，x2，
∴x1+x2=k，x1x2=-2，
又∵2（x1+x2）＞x1x2，
∴2k＞-2，即k＞-1．
点评：本题综合考查了根的判别式和根与系数的关系．
（2）由根与系数的关系x1+x2=-
、x1x2=来求k的取值范围．解答：解：（1）证明：由方程x2-kx-2=0知
a=1，b=-k，c=-2，
∴△=b2-4ac
=（-k）2-4×1×（-2）
=k2+8＞0，
∴无论k为何值时，方程有两个不相等的实数根；
（2）∵方程x2-kx-2=0．的两根为x1，x2，
∴x1+x2=k，x1x2=-2，
又∵2（x1+x2）＞x1x2，
∴2k＞-2，即k＞-1．
点评：本题综合考查了根的判别式和根与系数的关系．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
