Question

如图，已知A、B、C、D为圆上四点，弧AD、弧BC的度数分别为120°和40°，则∠E=________．

Answer 1

40°
分析：首先设圆心为O，连接OA，OB，OC，OD，BD，由弧AD、弧BC的度数分别为120°和40°，可得∠AOD=120°，∠BOC=40°，然后由圆周角定理，求得∠BDC与∠ABD的度数，继而求得答案．
解答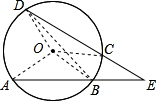：解：设圆心为O，连接OA，OB，OC，OD，BD，
∵弧AD、弧BC的度数分别为120°和40°，
∴∠AOD=120°，∠BOC=40°，
∴∠BDC=∠BOC=20°，∠ABD=∠AOD=60°，
∴∠E=∠ABD-∠BDC=40°．
故答案为：40°．
点评：此题考查了圆周角定理以及三角形外角的性质．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．