题目内容
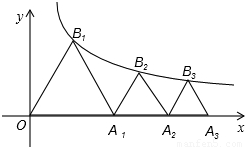
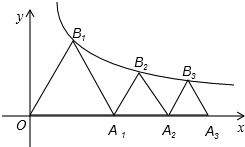 如图,B1(x1,y1)、B2(x2,y2),…,Bn(xn,yn)在函数y=
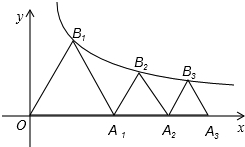
如图,B1(x1,y1)、B2(x2,y2),…,Bn(xn,yn)在函数y= (x>0)的图象上,△OB1A1,△B2A1A2,△B3A2A3,…,△BnAn-1An都是等边三角形,边OA1,A1A2,…,An-1An都在x轴上,则y1+y2+…+yn=________.
(x>0)的图象上,△OB1A1,△B2A1A2,△B3A2A3,…,△BnAn-1An都是等边三角形,边OA1,A1A2,…,An-1An都在x轴上,则y1+y2+…+yn=________.
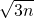
分析:作B1C⊥x轴,作B2D⊥x轴,作B3E⊥x轴,垂足分别为C、D、E点,根据∠B1OA1=60°可知tan60°=
 =
= ,设B1(a,
,设B1(a, a),代入反比例函数解析式可求a的值,再设A1D=b,表示B2的坐标,代入反比例函数解析式求b,由此寻找规律.
a),代入反比例函数解析式可求a的值,再设A1D=b,表示B2的坐标,代入反比例函数解析式求b,由此寻找规律.解答:
 解:作B1C⊥x轴,作B2D⊥x轴,作B3E⊥x轴,垂足分别为C、D、E点,
解:作B1C⊥x轴,作B2D⊥x轴,作B3E⊥x轴,垂足分别为C、D、E点,根据∠B1OA1=60°可知tan60°=
 =
= ,
,设B1(a,
 a),
a),代入函数y=
 中,得a•
中,得a• a=
a= ,
,解得a=1(舍去负值),
∴y1=
 ,
,设A1D=b,则B2(2+b,
 b),代入反比例函数解析式,得
b),代入反比例函数解析式,得(2+b)•
 b=
b= ,
,解得b=
 -1,
-1,∴y2=
 b=
b= -
- ,
,设A2E=c,则B3(2
 +c,
+c, c),代入反比例函数解析式,得
c),代入反比例函数解析式,得(2
 +c)•
+c)• c=
c= ,
,解得c=
 -
- ,
,∴y3=
 c=3-
c=3- ,
,∴y1+y2+…+yn=
 (a+b+c+…)=
(a+b+c+…)= (1+
(1+ -1+
-1+ -
- +…+
+…+ -
-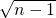 )=
)=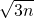 .
.故答案为:
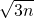 .
.点评:本题考查了反比例函数的综合运用.关键是根据反比例函数图象上点的坐标特点,等边三角形的性质,寻找纵坐标的一般规律.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 如图,B1(x1,y1)、B2(x2,y2),…,Bn(xn,yn)在函数y=
如图,B1(x1,y1)、B2(x2,y2),…,Bn(xn,yn)在函数y=
 如图在平面直角坐标系中,已知三点坐标分别是A(-1,0),B(-2,2),M(0,1).
如图在平面直角坐标系中,已知三点坐标分别是A(-1,0),B(-2,2),M(0,1).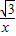 (x>0)的图象上,△OB1A1,△B2A1A2,△B3A2A3,…,△BnAn-1An都是等边三角形,边OA1,A1A2,…,An-1An都在x轴上,则y1+y2+…+yn= .
(x>0)的图象上,△OB1A1,△B2A1A2,△B3A2A3,…,△BnAn-1An都是等边三角形,边OA1,A1A2,…,An-1An都在x轴上,则y1+y2+…+yn= .