题目内容
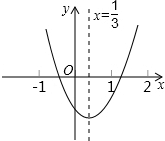
如图所示，二次函数y=ax2+bx+c（a≠0）的图象经过点（-1，2），且与x轴交点的横坐标分别为x1，x2，其中-2＜x1＜-1，0＜x2＜1，下列结论：①abc＞0；
②4a-2b+c＜0；
③2a-b＜0；
④b2+8a＞4ac．
其中正确的有（ ）
A．1个
B．2个
C．3个
D．4个
【答案】分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
解答：解：①∵该函数图象的开口向下，∴a＜0；
又对称轴x=-
＜0，
∴b＜0；
而该函数图象与y轴交于正半轴，故c＞0，
∴abc＞0，正确；
②当x=-2时，y＜0，即4a-2b+c＜0；正确；
③根据题意得，对称轴-1＜x=-
＜0，∴2a-b＜0，正确；
④∵
≥2，a＜0，
∴4ac-b2≤8a，
即b2+8a≥4ac，错误．
故选C．
点评：本题考查二次函数y=ax2+bx+c系数符号的确定由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定．
解答：解：①∵该函数图象的开口向下，∴a＜0；
又对称轴x=-
＜0，∴b＜0；
而该函数图象与y轴交于正半轴，故c＞0，
∴abc＞0，正确；
②当x=-2时，y＜0，即4a-2b+c＜0；正确；
③根据题意得，对称轴-1＜x=-
＜0，∴2a-b＜0，正确；④∵
≥2，a＜0，∴4ac-b2≤8a，
即b2+8a≥4ac，错误．
故选C．
点评：本题考查二次函数y=ax2+bx+c系数符号的确定由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定．
练习册系列答案
相关题目
小明从如图所示的二次函数y=ax2+bx+c的图象中，观察得出了下面六条信息：①c＜0；②abc＞0；③a-b+c＞0；④2a-3b=0；⑤4a+2b+c＞0；⑥一元二次方程ax2+bx+c=0有两异号实根．
你认为其中正确信息的个数有（ ）
| A、3个 | B、4个 | C、5个 | D、6个 |
铅球从A点被推出，实线部分表示铅球所经过的路线）
如图所示的二次函数y=ax2+bx+c的图象中，刘星同学观察得出了下面四条信息：
如图所示，二次函数 y=ax2+bx+c的图象与x轴交于点A和点B（A、B分别位于原点O的两侧），与y轴的下半轴交于点C，且tan∠OAC=2，AB=CB=5．
（2012•甘谷县模拟）如图所示是二次函数y=ax2+bx+c图象的一部分，图象过A点（3，0），对称轴为x=1，给出四个结论：①b2-4ac＞0；②2a+b=0；③a+b+c=0；④当x=-1或x=3时，函数y的值都等于0．把正确结论的序号填在横线上