题目内容
 如图,在平面直径坐标系内,点A的坐标(10,0),点B在第一象限内,BO=5,sin∠BOA=0.6,求:
如图,在平面直径坐标系内,点A的坐标(10,0),点B在第一象限内,BO=5,sin∠BOA=0.6,求:(1)点B的坐标;
(2)sin∠BAO的值.
考点:解直角三角形,坐标与图形性质
专题:
分析:(1)作BC⊥OA,根据BO和sin∠BOA即可求得BC的值,根据勾股定理即可求得OC的长,即可解题;
(2)根据(1)中OC的长可求得AC的长,根据勾股定理可以求得AB的长,即可解题.
(2)根据(1)中OC的长可求得AC的长,根据勾股定理可以求得AB的长,即可解题.
解答:解:(1)作BC⊥OA,

∵BO=5,sin∠BOA=0.6,
∴BC=3,
∴OC=
=4,
∴点B坐标(4,3);
(2)∵OA=10,OC=4,
∴AC=6,
∴AB=
=3
,
∴sin∠BAO=
=
.

∵BO=5,sin∠BOA=0.6,
∴BC=3,
∴OC=
| OB2-BC2 |
∴点B坐标(4,3);
(2)∵OA=10,OC=4,
∴AC=6,
∴AB=
| AC2+BC2 |
| 5 |
∴sin∠BAO=
| BC |
| AB |
| ||
| 5 |
点评:本题考查了直角三角形中勾股定理的运用,考查了三角函数在直角三角形中运用,考查了三角函数的求值,本题中求得BC,AC的长是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
一个三角形的两边长分别为3cm和7cm,则此三角形第三边长可能是( )
| A、3cm | B、4cm |
| C、7cm | D、11cm |
 尺规作图.
尺规作图. 某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的: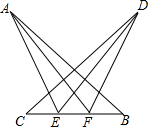 如图所示,已知AB=DC,AE=DF,CE=BF,试说明:AF=DE.
如图所示,已知AB=DC,AE=DF,CE=BF,试说明:AF=DE.