题目内容
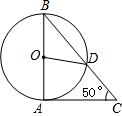
如图，PA、PB切⊙O于A、B，∠APB=60゜，PA=4，则⊙O的半径为______．
连接OA、OP
∵PA、PB是⊙O的切线
∴∠OAP=90°，∠APO=
∠APB=30°
Rt△OAP中，
∵tan∠APO=
∴OA=PA•tan30°=4×
=
．
故答案是：
．
∵PA、PB是⊙O的切线
∴∠OAP=90°，∠APO=
| 1 |
| 2 |
Rt△OAP中，
∵tan∠APO=
| OA |
| PA |
∴OA=PA•tan30°=4×
| ||
| 3 |
4
| ||
| 3 |
故答案是：
4
| ||
| 3 |
练习册系列答案
同步练习强化拓展系列答案
相关题目
