题目内容
18. 如图,在平面直角坐标系中,直线y=-2x+4与x轴和y轴分别交于点A和点B,另有一点M,其坐标为(m,n),若直线OM将△OAB分成面积相等的两部分,则m与n的关系为( )
如图,在平面直角坐标系中,直线y=-2x+4与x轴和y轴分别交于点A和点B,另有一点M,其坐标为(m,n),若直线OM将△OAB分成面积相等的两部分,则m与n的关系为( )| A. | m=2n | B. | m=$\frac{n}{2}$ | C. | m=n | D. | m=n+1 |
分析 先求出A、B两点的坐标,再根据直线OM将△OAB分成面积相等的两部分可知M为线段AB的中点,进而可得出结论.
解答 解:∵当x=0时,y=4;当y=0时,x=2,
∴A(2,0),B(0,4).
∵直线OM将△OAB分成面积相等的两部分,
∴M为线段AB的中点,
∴m=$\frac{2+0}{2}$=1,n=$\frac{0+4}{2}$=2,即m=$\frac{n}{2}$.
故选B.
点评 本题考查的是一次函数的性质,熟知一次函数图象上点的坐标特点是解答此题的关键.

练习册系列答案
相关题目
9.下列说法正确的是( )
| A. | 小强今年12岁,明年百分之二百地是13岁 | |
| B. | 同时抛掷两枚硬币,同是正面或同是反面朝上的可能性比一正一反大 | |
| C. | 两个不透明的布袋中都放有除颜色外完全相同的球,甲布袋有6个红球,乙布袋中有8个红球,那么在甲、乙两布袋中各任意摸一球,从乙布袋中摸到红球的概率大 | |
| D. | 盒子里装有10个完全相同的纸团,只有一个纸团内写有“奖”,而另九个纸团内均为“谢谢惠顾”,10名参与者可从中任摸一个纸团,则先摸的和后摸的“中奖”概率一样大 |
6.某商场将进货单价为18元的商品,按每件20元售出时,每天可销售100件,如果每件提高1元,日销售量就要减少10件,若使商场投资少,收益大,那么该商品的售出价格定为多少元时,才能使每天获得350元?
10.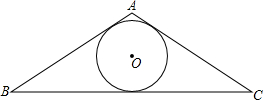 已知:如图,⊙O是△ABC的内切圆,下列说法错误的是( )
已知:如图,⊙O是△ABC的内切圆,下列说法错误的是( )
 已知:如图,⊙O是△ABC的内切圆,下列说法错误的是( )
已知:如图,⊙O是△ABC的内切圆,下列说法错误的是( )| A. | 点O在△ABC的三边垂直平分线上 | |
| B. | 点O在△ABC的三个内角平分线上 | |
| C. | 如果△ABC的面积为S,三边长为a,b,c,⊙O的半径为r,那么r=$\frac{2S}{a+b+c}$ | |
| D. | 如果△ABC的三边长分别为5,7,8,那么以A、B、C为端点三条切线长分别为5,3,2 |
 如图,四边形ABCD中,∠ADB=∠DBC=90°,AD=6,CD=12,tanA=$\frac{4}{5}$,求sinC的值.
如图,四边形ABCD中,∠ADB=∠DBC=90°,AD=6,CD=12,tanA=$\frac{4}{5}$,求sinC的值. 如图,在△ABC中,AB=AC,∠A=42°,AB的垂直平分线MN交AC于点D.求∠DBC的度数.
如图,在△ABC中,AB=AC,∠A=42°,AB的垂直平分线MN交AC于点D.求∠DBC的度数.