题目内容

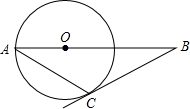
如图，直线PM切⊙O于点M，直线PO交⊙O于A、B两点，弦AC∥PM，连接OM、BC．
求证：（1）△ABC∽△POM；（2）2OA2=OP•BC．
证明：（1）∵直线PM切⊙O于点M，
∴∠PMO=90°，
∵弦AB是直径，
∴∠ACB=90°，
∴∠ACB=∠PMO，
∵AC∥PM，
∴∠CAB=∠P，
∴△ABC∽△POM；

（2）∵△ABC∽△POM，
∴
AB
PO
=
BC
OM
，
又AB=2OA，OA=OM，
∴
2OA
PO
=
BC
OA
，
∴2OA2=OP•BC．
练习册系列答案
相关题目
已知：如图，BC是⊙O的切线，C是切点，AC是⊙O的弦，AO的延长线交BC于点B，设⊙O的半径为
5
，∠ACB=120°．求AB的长．
如图，∠PAQ是直角，⊙O与AP相切于点T，与AQ交于B、C两点．
（1）BT是否平分∠OBA，说明你的理由；
（2）若已知AT=4，弦BC=6，试求⊙O的半径R．
如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于点E．
（1）求证：点E是边BC的中点；
（2）若EC=3，BD=2
6
，求⊙O的直径AC的长度；
（3）若以点O，D，E，C为顶点的四边形是正方形，试判断△ABC的形状，并说明理由．
如图，⊙O的半径为6cm，经过⊙O上一点C作⊙O的切线交半径OA的延长于点B，作∠ACO的平分线交⊙O于点D，交OA于点F，延长DA交BC于点E．
（1）求证：AC∥OD；
（2）如果DE⊥BC，求
AC
的长度．
如图的⊙A和⊙B是抗日战争时期敌人要塞阵地的两个“母子碉堡”，被称为“母碉堡”A的半径是6米，“子碉堡”B的半径是3米，两个碉堡中心的距离AB=80米．我侦察兵在安全地带P的视线恰好与敌人的“母子碉堡”都相切，为了打击敌人，必须准确地计算出点P到敌人两座碉堡中心的距离PA和PB的大小，请你利用圆的知识计算出PA=______，PB=______．
已知：在⊙O中，AB是直径，AC是弦，OE⊥AC于点E，过点C作直线FC，使∠FCA=∠AOE，交AB的延长线于点D．
（1）求证：FD是⊙O的切线；
（2）设OC与BE相交于点G，若OG=2，求⊙O半径的长；
（3）在（2）的条件下，当OE=3时，求图中阴影部分的面积．
如图1，AB是⊙O的直径，射线BM⊥AB，垂足为B，点C为射线BM上的一个动点（C与B不重合），连接AC交⊙O于D，过点D作⊙O的切线交BC于E．
（1）在C点运动过程中，当DE∥AB时（如图2），求∠ACB的度数；
（2）在C点运动过程中，试比较线段CE与BE的大小，并说明理由；
（3）∠ACB在什么范围内变化时，线段DC上存在点G，满足条件BC2=4DG•DC（请写出推理过程）．
如图，AB是⊙O的直径，弦DC交AB于E，过C作⊙O的切线交DB的延长线于M，若AB=4，∠ADC=45°，∠M=75°，则CD的长为（　　）
A．
3
B．2C．3
3
D．2
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网