题目内容
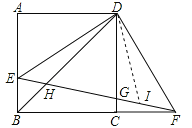
【题目】如图,正方形ABCD中,E为AB边上一点,过点D作DF⊥DE,与BC延长线交于点F.连接EF,与CD边交于点G,与对角线BD交于点H.
(1)若BF=BD=![]() ,求BE的长;
,求BE的长;
(2)若∠ADE=2∠BFE,求证:FH=HE+HD.

【答案】(1)BE=2-![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】分析:(1)由四边形ABCD正方形,BF=BD=![]() ,由勾股定理即可求得BC的长,又由DF⊥DE,易证得△ADE≌△CDF,即可求得BE的长;
,由勾股定理即可求得BC的长,又由DF⊥DE,易证得△ADE≌△CDF,即可求得BE的长;
(2)首先在FE上截取一段FI,使得FI=EH,由△ADE≌△CDF,易证得△DEH≌△DFI,即可得DH=DI,又由∠ADE=2∠BFE,易证得△DHI为等边三角形,即可得DH=HI,继而可得FH=HE+HD.
详解:(1)解:∵四边形ABCD正方形,∴∠BCD=90°,BC=CD,∴Rt△BCD中,BC2+CD2=BD2,即BC2=(![]() )2﹣(BC)2,∴BC=AB=1.∵DF⊥DE,∴∠ADE+∠EDC=90°=∠EDC+∠CDF,∴∠ADE=∠CDF.在△ADE和△CDF中,∵
)2﹣(BC)2,∴BC=AB=1.∵DF⊥DE,∴∠ADE+∠EDC=90°=∠EDC+∠CDF,∴∠ADE=∠CDF.在△ADE和△CDF中,∵ ,∴△ADE≌△CDF(ASA),∴AE=CF=BF﹣BC=
,∴△ADE≌△CDF(ASA),∴AE=CF=BF﹣BC=![]() ﹣1,∴BE=AB﹣AE=1﹣(
﹣1,∴BE=AB﹣AE=1﹣(![]() ﹣1)=2﹣
﹣1)=2﹣![]() ;
;
(2)证明:在FE上截取一段FI,使得FI=EH.∵△ADE≌△CDF,∴DE=DF,∴△DEF为等腰直角三角形,∴∠DEF=∠DFE=45°=∠DBC.∵∠DHE=∠BHF,∴∠EDH=∠BFH(三角形的内角和定理).在△DEH和△DFI中,∵ ,∴△DEH≌△DFI(SAS),∴DH=DI.又∵∠HDE=∠BFE,∠ADE=2∠BFE,∴∠HDE=∠BFE=
,∴△DEH≌△DFI(SAS),∴DH=DI.又∵∠HDE=∠BFE,∠ADE=2∠BFE,∴∠HDE=∠BFE=![]() ∠ADE.∵∠HDE+∠ADE=45°,∴∠HDE=15°,∴∠DHI=∠DEH+∠HDE=60°,即△DHI为等边三角形,∴DH=HI,∴FH=FI+HI=HE+HD.
∠ADE.∵∠HDE+∠ADE=45°,∴∠HDE=15°,∴∠DHI=∠DEH+∠HDE=60°,即△DHI为等边三角形,∴DH=HI,∴FH=FI+HI=HE+HD.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案