题目内容
如图4，已知⊙O是△ABC的外接圆，AB为直径，若PA⊥AB，PO过AC的中点M，
求证：PC是⊙O的切线．
证明：连接OC，
∵PA⊥AB， ∴∠PA0=900，
∵PO过AC的中点M，OA=OC，
∴PO平分∠AOC，
∴∠AOP=∠COP .
∴在△PAO与△PCO中有
OA=OC，∠AOP=∠COP，PO=PO,
∴△PAO≌△PCO,
∴∠PCO=∠PA0=900,
即PC是⊙O的切线．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
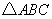为格点三角形（即三角形的顶点都在格点上）．
方向平移后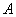，点
移到点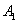
，在网格中画出平移后得到的
；
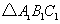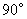，在网格中画出旋转后的
；
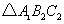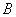经过（1）、（2）变换的路径总长．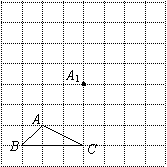
，其中
满足
.
C．
D．2
＝ ．
，底面圆的半
，则圆锥的侧面积为 
．（结果用
表示）
经过（—2，0）、（1，6），求不等式
的解集。