题目内容
6.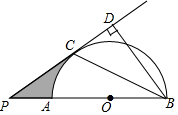 如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC
如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC(1)求证:BC平分∠PBD;
(2)求证:PC2=PA•PB;
(3)若PA=2,PC=2$\sqrt{3}$,求阴影部分的面积(结果保留π)
分析 (1)连接OC,由PD切⊙O于点C,得到OC⊥PD,根据平行线的性质得到∠DBC=∠BCO,根据的预计实现的性质得到∠OCB=∠OBC,等量代换得到∠OBC=∠CBD,于是得到即可;
(2)连接AC,由AB是半圆O的直径,得到∠ACB=90°,推出∠ACP=∠ABC,根据相似三角形的性质即可得到结论;
(3)根据图形的面积公式即可得到结果.
解答 解:(1)连接OC,
∵PD切⊙O于点C,
∴OC⊥PD,
∵BD⊥PD,
∴BD∥OC,
∴∠DBC=∠BCO,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OBC=∠CBD,
∴BC平分∠PBD;
(2)连接AC,
∵AB是半圆O的直径,
∴∠ACB=90°,
∴∠ACO+∠BCO=∠ACO+∠ABC=90°,
∵∠PCA+∠ACO=90°,
∴∠ACP=∠ABC,
∵∠P=∠P,
∴△ACP∽△CBP,
∴$\frac{PC}{PB}=\frac{PA}{PC}$,
∴PC2=PA•PB;
(3)∵PC2=PA•PB,PA=2,PC=2$\sqrt{3}$,
∴PB=6,
∴AB=4,
∴OC=2,PO=4,
∴∠POC=60°,
∴S阴影=S△POC-S扇形=$\frac{1}{2}×$2$\sqrt{3}$×2-$\frac{60•π×{2}^{2}}{360}$=2$\sqrt{3}$-$\frac{2}{3}$π.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,平行线的性质,角平分线的定义,扇形面积的计算,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.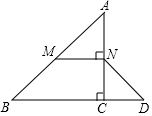 如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=$\frac{1}{3}$BD,连接DN、MN.若AB=6.
如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=$\frac{1}{3}$BD,连接DN、MN.若AB=6.
(1)求证:MN=CD;
(2)求DN的长.
 如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=$\frac{1}{3}$BD,连接DN、MN.若AB=6.
如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=$\frac{1}{3}$BD,连接DN、MN.若AB=6.(1)求证:MN=CD;
(2)求DN的长.
14.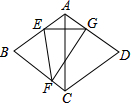 如图,在菱形ABCD中,∠BAD=120°,将菱形沿EF折叠,点B正好落在AD边的点G处,且EG⊥AC,若CD=8,则FG的长为( )
如图,在菱形ABCD中,∠BAD=120°,将菱形沿EF折叠,点B正好落在AD边的点G处,且EG⊥AC,若CD=8,则FG的长为( )
 如图,在菱形ABCD中,∠BAD=120°,将菱形沿EF折叠,点B正好落在AD边的点G处,且EG⊥AC,若CD=8,则FG的长为( )
如图,在菱形ABCD中,∠BAD=120°,将菱形沿EF折叠,点B正好落在AD边的点G处,且EG⊥AC,若CD=8,则FG的长为( )| A. | 4$\sqrt{2}$ | B. | 4$\sqrt{3}$ | C. | 4$\sqrt{6}$ | D. | 6 |
1.“3.15“植树节活动后,某校对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测,以下是根据观测数据制成的统计图表的一部分;
表1:栽下的各品种树苗棵数统计表表
请你根据以上信息解答下列问题:
(1)这次栽下的四个品种的树苗共500棵,乙品种树苗100棵.
(2)图1中,甲30%、乙20%;
(3)已知这批树苗成活率为90%,将图2补充完整.
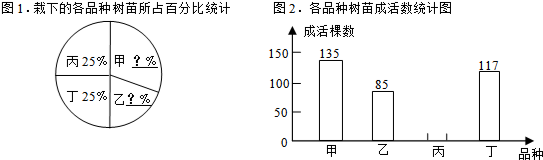
表1:栽下的各品种树苗棵数统计表表
| 植树品种 | 甲种 | 乙种 | 丙种 | 丁种 |
| 植树棵数 | 150 | 125 | 125 |
(1)这次栽下的四个品种的树苗共500棵,乙品种树苗100棵.
(2)图1中,甲30%、乙20%;
(3)已知这批树苗成活率为90%,将图2补充完整.

15.已知点P(x+3,x-4)在y轴上,则x的值为( )
| A. | 3 | B. | -3 | C. | -4 | D. | 4 |
16. 实数a,b,c在数轴上的对应点的位置如图所示,则a的相反数是( )
实数a,b,c在数轴上的对应点的位置如图所示,则a的相反数是( )
 实数a,b,c在数轴上的对应点的位置如图所示,则a的相反数是( )
实数a,b,c在数轴上的对应点的位置如图所示,则a的相反数是( )| A. | a | B. | b | C. | -b | D. | c |
 如图,反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=$\frac{1}{4}$x的图象交于点A、B,点B的横坐标是4,点P(1,m)在反比例函数y1=$\frac{k}{x}$的图象上.
如图,反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=$\frac{1}{4}$x的图象交于点A、B,点B的横坐标是4,点P(1,m)在反比例函数y1=$\frac{k}{x}$的图象上. 如图,一次函数y=kx+b(k≠0)的图象过点P(-$\frac{3}{2}$,0),且与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A(-2,1)和点B.
如图,一次函数y=kx+b(k≠0)的图象过点P(-$\frac{3}{2}$,0),且与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A(-2,1)和点B.