��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У���A��8��0����B���ڵ�һ���ޣ�BO=BA=5����M��N��OB��OA�е㣬��1��ֱ��MN�Ľ���ʽΪ
��2����ABN���=
��3����ͼ��1���еġ�NMO�Ƶ�O��תһ�ܣ�����ת�����У���ABN����Ƿ�������ֵ����Сֵ���������ڣ���˵�����ɣ����������ڱ���ͼ�л�����Ӧλ�õ�ͼ�Σ���ֱ��д�����ֵ����Сֵ��
��4����ͼ��1���еġ�NMO�Ƶ�O��ת������N�ڵڶ�����ʱ����ͼ��2������N��x��y������ABN�����ΪS����S��x֮��ĺ�����ϵʽ��
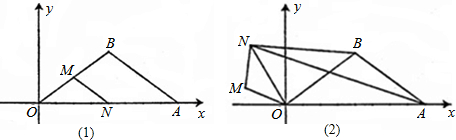
��������1��Ҫ��MN�Ľ���ʽ��Ҫ�뷨�����M��N�����꣬N���е㣬���������N������꣬��MC��OA��ͨ����ֱ�������ο������M�����꣬�Ӷ����ֱ��MN�Ľ���ʽ��
��2������MN��N���е㣬OB=AB��˵����AOB�ǵ��������Σ����ݵ��������ε����ʿ���֪��BN��OA�������ù��ɶ����������BN�ij��ȣ��Ӷ����������ABN�������
��3������ת�Ĺ����У���N�������߶�OB��ʱ����ABN�������С����N�������߶�OB�ķ����ӳ�����ʱ����ABN���������Ը��������ʽ�����ֵ��
��4������N��OA�Ĵ��߽�OA��E����AB���ӳ����ڵ�F�����EF��ED��AE�ij��ȣ�����S��ANF��ȥS��BNF���ǡ�ABN�������
��2������MN��N���е㣬OB=AB��˵����AOB�ǵ��������Σ����ݵ��������ε����ʿ���֪��BN��OA�������ù��ɶ����������BN�ij��ȣ��Ӷ����������ABN�������
��3������ת�Ĺ����У���N�������߶�OB��ʱ����ABN�������С����N�������߶�OB�ķ����ӳ�����ʱ����ABN���������Ը��������ʽ�����ֵ��
��4������N��OA�Ĵ��߽�OA��E����AB���ӳ����ڵ�F�����EF��ED��AE�ij��ȣ�����S��ANF��ȥS��BNF���ǡ�ABN�������
��� �⣺��1����MC��OA��C
�⣺��1����MC��OA��C
��A��8��0��
��OA=8
��M��N��OA��OB���е�
��MN�ǡ�AOB����λ�ߣ�ON=AN=4��OM=BM=
��MN=
AB=
��N��4��0��
��OM=MN
��OC=NC=2����Rt��OCM�У��ɹ��ɶ����ã�
MC=
��M��2��
��
�裺y=kx+b���������
��ã�
��MN�Ľ���ʽΪ��y=-
x+3
��2����
=
����MC=

��BN=3
��S��ABN=
=6
��3����N�㵽��G��ʱ��ANB�������СΪ��
��N�㵽��H��ʱ��ANB��������Ϊ��
��4������N��NF��OA��E��AB���ӳ����ڵ�F��BD��OA��A
��BD=3��OD=AD=4
��N��x��y������N�ڵڶ�����
��NE=y��EO=-x
��AE=8-x
��NF��OA��BD��OA
��ADB���ס�AEF
��
=
��
=
��EF=
��Rt��NEO���ɹ��ɶ����ã�
y2+��-x��2=42
��y=
NF=
-
��S��ABN=S��AFN-S��NBF
��S��ABN=
-
��S=
��
 �⣺��1����MC��OA��C
�⣺��1����MC��OA��C��A��8��0��
��OA=8
��M��N��OA��OB���е�
��MN�ǡ�AOB����λ�ߣ�ON=AN=4��OM=BM=
| 5 |
| 2 |
��MN=
| 1 |
| 2 |
| 5 |
| 2 |
��OM=MN
��OC=NC=2����Rt��OCM�У��ɹ��ɶ����ã�
MC=
| 3 |
| 2 |
��M��2��
| 3 |
| 2 |
�裺y=kx+b���������
|
|
��MN�Ľ���ʽΪ��y=-
| 3 |
| 4 |
��2����
| MC |
| BN |
| 1 |
| 2 |
| 3 |
| 2 |

��BN=3
��S��ABN=
| 3��4 |
| 2 |
��3����N�㵽��G��ʱ��ANB�������СΪ��
| 12 |
| 5 |
��N�㵽��H��ʱ��ANB��������Ϊ��
| 108 |
| 5 |
��4������N��NF��OA��E��AB���ӳ����ڵ�F��BD��OA��A
��BD=3��OD=AD=4
��N��x��y������N�ڵڶ�����

��NE=y��EO=-x
��AE=8-x
��NF��OA��BD��OA
��ADB���ס�AEF
��
| DB |
| EF |
| AD |
| AE |
��
| 3 |
| EF |
| 4 |
| 8-x |
��EF=
| 24-3x |
| 4 |
��Rt��NEO���ɹ��ɶ����ã�
y2+��-x��2=42
��y=
| 16-x2 |
NF=
| 24-3x |
| 4 |
| 16-x2 |
��S��ABN=S��AFN-S��NBF
��S��ABN=
(
| ||||
| 2 |
(
| ||||
| 2 |
��S=
24-3x-4
| ||
| 2 |
������������һ��һ�κ������ۺ����⣬�����������������������Ľ���ʽ�������ε��������ת�����е�������ֵ����Сֵ����һ���ۺ��Խ�ǿ�����⣮

��ϰ��ϵ�д�
 ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д� ��ĩ�óɼ�ϵ�д�
��ĩ�óɼ�ϵ�д�
�����Ŀ
 ��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD��
��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD�� ��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ�����
��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ����� ��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ
��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ��������� ��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��