题目内容
14. 如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的矩形花圃,设花圃的边AB的长为x(m),面积为y(m2).
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的矩形花圃,设花圃的边AB的长为x(m),面积为y(m2).(1)若y与x之间的函数关系式;
(2)若要围成面积为45m2的花圃,AB的长是多少米?
(3)能围成面积比45m2更大的花圃吗?若能,请求出最大面积,并说明围法;若不能,请说明理由.
分析 (1)由矩形的面积公式即可得出结果;
(2)把y=45代入函数关系式,解方程结果;
(3)由二次函数的解析式得出y的最大值即可.
解答 解:(1)根据题意得:∵y=x(24-3x)═-3x2+24x,
∴y=-3x2+24x;
(2)当y=45时,-3x2+24x=45,
解得:x=3或x=5,
当x=3时,24-3x=15>10,
∴x=3不合题意舍去,
∴x=5,即AB的长是5米;
(3)可以;理由如下:
∵y=-3x2+24x=-3(x-4)2+48,-3<0,
∴y有最大值,
当x=4时,y的最大值=48,
即围成花圃的最大面积为48m2.
点评 本题考查了二次根式的应用、二次函数的最值、一元二次方程的运用;根据题意得出函数关系式是解决问题的关键.

练习册系列答案
相关题目
5.下列运算正确的是( )
| A. | a3+a3=2a3 | B. | a6÷a3=a2 | C. | (3a3)2=6a6 | D. | 2(a+1)=2a+1 |
6.已知a,b,c是△ABC的三边长,且满足|a-b|+$\sqrt{c-b}$=0,则是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 不能确定 |
4.某机械厂七月份的营业额为100万元,已知第三季度的总营业额共331万元.如果平均每月增长率为x,则由题意列方程应为( )
| A. | 100(1+x)2=331 | B. | 100+100×2x=331 | ||
| C. | 100+100×3x=331 | D. | 100[1+(1+x)+(1+x)2]=331 |
 如图,△ABC中,AB=41,BC=15,CA=52,AM平分∠BAC,点D、E分别为AM、AB上的动点,则BD+DE的最小值是9.
如图,△ABC中,AB=41,BC=15,CA=52,AM平分∠BAC,点D、E分别为AM、AB上的动点,则BD+DE的最小值是9.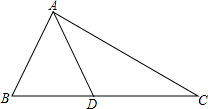 如图,在△ABC中,D为BC边上一点,AB=AD=DC.
如图,在△ABC中,D为BC边上一点,AB=AD=DC.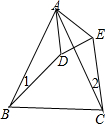 已知∠BAC=∠DAE,∠1=∠2,BD=CE.问△ABD≌△ACE吗?为什么?
已知∠BAC=∠DAE,∠1=∠2,BD=CE.问△ABD≌△ACE吗?为什么?