题目内容
如图,已知A(x1,y1),B(x2,y2)是双曲线y=
在第一象限内的分支上的两点,连接OA、OB.
(1)试说明y1<OA<y1+
;
(2)过B作BC⊥x轴于C,当k=4时,求△BOC的面积.
| k |
| x |
(1)试说明y1<OA<y1+
| k |
| y1 |
(2)过B作BC⊥x轴于C,当k=4时,求△BOC的面积.

(1)过点A作AD⊥x轴于D,
则OD=x1,AD=y1,
因为点A(x1,y1)在双曲线y=
上,
故x1=
,
又在Rt△OAD中,
AD<OA<AD+OD,
所以y1<OA<y1+
;
(2)△BOC的面积为;
×4=2.
则OD=x1,AD=y1,
因为点A(x1,y1)在双曲线y=
| k |
| x |
故x1=
| k |
| y1 |
又在Rt△OAD中,
AD<OA<AD+OD,
所以y1<OA<y1+
| k |
| y1 |
(2)△BOC的面积为;
| 1 |
| 2 |

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
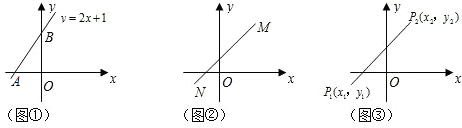
 如图,已知A(x1,y1),B(x2,y2)是双曲线y=
如图,已知A(x1,y1),B(x2,y2)是双曲线y= 如图,已知A(x1,y1),B(x2,y2)是双曲线y=
如图,已知A(x1,y1),B(x2,y2)是双曲线y= 在第一象限内的分支上的两点,连接OA、OB.
在第一象限内的分支上的两点,连接OA、OB. ;
;