题目内容

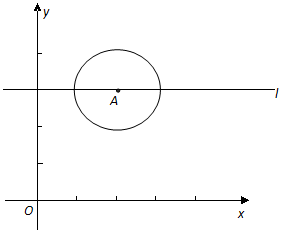
如图，已知为坐标原点，点的坐标为，的半径为1，过作直线平行于轴，点在上运动．

（1）当点运动到圆上时，求线段的长．

（2）当点的坐标为时，试判断直线与的位置关系，并说明理由．

 

【答案】

解：（1）如图，设与轴交点为

当点运动到圆上时，有两个位置

，

（2）连接，过作，垂足为

，

在中，

，

直线与相离．

【解析】（1）画出图形可知点所在的位置两种情况，利用直角三角形的勾股定理即可求出线段的长

（2）判断直线与圆的位置关系，是要比较圆心到直线的距离与圆的半径之间的大小，过作，垂足为，利用勾股定理及相似三角形的对应边成比例，求出的即可，由于，故直线与相离

 

练习册系列答案
相关题目
如图，已知过坐标原点的抛物线经过A（x1，0），B（x2，3）两点，且x1、x2是方程x2+5x+6=0两根（x1＞x2），抛物线顶点为C．
（1）求抛物线的解析式；
（2）若点D在抛物线上，点E在抛物线的对称轴上，且以A、O、D、E为顶点的四边形是平行四边形，求点E的坐标；
（3）P是抛物线上的动点，过点P作PM⊥x轴，垂足为M，是否存在点P使得以点P、M、O为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．

如图，已知○为坐标原点，∠AOB＝30°，∠ABO＝90°，且点A的坐标为(2，0)．

(1)求点B的坐标；

(2)若二次函数y＝ax＋bx＋c的图象经过A、B、O三点，求此二次函数的解析式；

(3)在(2)中的二次函数图象的OB段(不包括点O、B)上，是否存在一点C，使得四边形ABCO的面积最大？若存在，求出这个最大值及此时点C的坐标；若不存在，请说明理由．

如图，已知为坐标原点，点的坐标为，的半径为1，过作直线平行于轴，点在上运动．
（1）当点运动到圆上时，求线段的长．
（2）当点的坐标为时，试判断直线与的位置关系，并说明理由．
如图，已知过坐标原点的抛物线经过A（x1，0），B（x2，3）两点，且x1、x2是方程x2+5x+6=0两根（x1＞x2），抛物线顶点为C．
（1）求抛物线的解析式；
（2）若点D在抛物线上，点E在抛物线的对称轴上，且以A、O、D、E为顶点的四边形是平行四边形，求点E的坐标；
（3）P是抛物线上的动点，过点P作PM⊥x轴，垂足为M，是否存在点P使得以点P、M、O为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网