题目内容
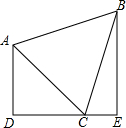 如图,直角梯形ADEB中,∠D=∠E=90°,△ABC是等边三角形,C点在DE上,AD=7,BE=11,则等边△ABC的面积是________.
如图,直角梯形ADEB中,∠D=∠E=90°,△ABC是等边三角形,C点在DE上,AD=7,BE=11,则等边△ABC的面积是________.
31
分析:作AF⊥BE交BE于F,设CE长为x,DC长为y,根据AB=AC=BC及勾股定理可得到关于xy的方程,求得xy的值,再根据△ABC的面积=梯形的面积-△ADC的面积-△BEC的面积计算求解即可.
解答: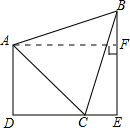 解:如图作AF⊥BE交BE于F,设CE长为x,DC长为y,则AF=DE,AD=EF.
解:如图作AF⊥BE交BE于F,设CE长为x,DC长为y,则AF=DE,AD=EF.
根据勾股定理得:AD2+DC2=AC2,CE2+BE2=BC2,AF2+BF2=AB2,
即72+y2=AC2,x2+112=BC2,(x+y)2+(11-7)2=AB2,
∵△ABC是等边三角形,即AB=AC=BC,
∴y2-x2=72,x2+2xy=33,
解得x= ,y=5
,y=5 .则DE=6
.则DE=6 .
.
∴△ABC的面积=梯形的面积-△ADC的面积-△BEC的面积
= (7+11)×6
(7+11)×6 -
- ×
× ×11-
×11- ×5
×5 ×7=31
×7=31 .
.
故答案填:31 .
.
点评:本题考查了直角梯形、等边三角形的性质及勾股定理的应用,解决此类题要懂得用梯形的常用辅助线,把梯形分割为矩形和直角三角形,从而由矩形和直角三角形的性质来求解.

分析:作AF⊥BE交BE于F,设CE长为x,DC长为y,根据AB=AC=BC及勾股定理可得到关于xy的方程,求得xy的值,再根据△ABC的面积=梯形的面积-△ADC的面积-△BEC的面积计算求解即可.
解答:
 解:如图作AF⊥BE交BE于F,设CE长为x,DC长为y,则AF=DE,AD=EF.
解:如图作AF⊥BE交BE于F,设CE长为x,DC长为y,则AF=DE,AD=EF.根据勾股定理得:AD2+DC2=AC2,CE2+BE2=BC2,AF2+BF2=AB2,
即72+y2=AC2,x2+112=BC2,(x+y)2+(11-7)2=AB2,
∵△ABC是等边三角形,即AB=AC=BC,
∴y2-x2=72,x2+2xy=33,
解得x=
 ,y=5
,y=5 .则DE=6
.则DE=6 .
.∴△ABC的面积=梯形的面积-△ADC的面积-△BEC的面积
=
 (7+11)×6
(7+11)×6 -
- ×
× ×11-
×11- ×5
×5 ×7=31
×7=31 .
.故答案填:31
 .
.点评:本题考查了直角梯形、等边三角形的性质及勾股定理的应用,解决此类题要懂得用梯形的常用辅助线,把梯形分割为矩形和直角三角形,从而由矩形和直角三角形的性质来求解.

练习册系列答案
相关题目
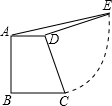 如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=3,BC=5,将腰DC绕点D逆时针方向旋转90°至DE,连接AE,则△ADE的面积是( )
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=3,BC=5,将腰DC绕点D逆时针方向旋转90°至DE,连接AE,则△ADE的面积是( )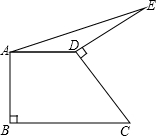 如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=3,BC=5.DE⊥CD,且DE=CD,连AE,则△ADE的面积为( )
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=3,BC=5.DE⊥CD,且DE=CD,连AE,则△ADE的面积为( )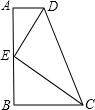 如图,直角梯形ABCD中,AB⊥BC,AD∥BC,点E是AB的中点,且AD+BC=DC、下列结论中:①△ADE∽△BEC;②DE2=DA•DC;③若设AD=a,CD=b,BC=c,则关于x的方程ax2+bx+c=0有两个不相等的实数根;④若设AD=a,AB=b,BC=c,则关于x的方程ax2+bx+c=0有两个相等的实数根.其中正确的结论有( )个.
如图,直角梯形ABCD中,AB⊥BC,AD∥BC,点E是AB的中点,且AD+BC=DC、下列结论中:①△ADE∽△BEC;②DE2=DA•DC;③若设AD=a,CD=b,BC=c,则关于x的方程ax2+bx+c=0有两个不相等的实数根;④若设AD=a,AB=b,BC=c,则关于x的方程ax2+bx+c=0有两个相等的实数根.其中正确的结论有( )个.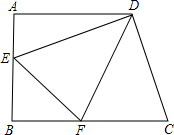 如图,直角梯形ABCD中,AD∥BC,∠A=90°,AB=AD=6,DE⊥DC交AB于E,DF平分∠EDC交BC于F,连接EF.
如图,直角梯形ABCD中,AD∥BC,∠A=90°,AB=AD=6,DE⊥DC交AB于E,DF平分∠EDC交BC于F,连接EF.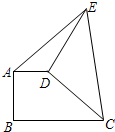 如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,将腰CD以D为中心逆时针旋转90°至DE,连结AE、CE,△ADE的面积为12,则BC的长为
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,将腰CD以D为中心逆时针旋转90°至DE,连结AE、CE,△ADE的面积为12,则BC的长为