题目内容
是否存在一个三位数. |
| abc |
. |
| abc |
. |
| bca |
. |
| cab |
分析：假设存在，那么三数之和可写成111（a+b+c），由于111（a+b+c）完全平方数，而111=3×37，且3、37是质数，故可知a+b+c中必有因数3和37，又0≤a+b+c≤27，说明a+b+c中不含因数37，从而
+
+
不是完全平方数，这样的三位数不存在．
. |
| abc |
. |
| bca |
. |
| cab |
解答：解：假设存在，根据题意得
+
+
=100a+10b+c+100b+10c+a+100c+10a+b=111（a+b+c），
∵111=3×37，
而3、37是质数，
∴a+b+c的和中必有因数3和37，
又a，b，c取从1到9的自然数，
∴0≤a+b+c≤27，
∴a+b+c中不含因数37，
∴
+
+
不是完全平方数．
故这样的三位数不存在．
. |
| abc |
. |
| bca |
. |
| cab |
∵111=3×37，
而3、37是质数，
∴a+b+c的和中必有因数3和37，
又a，b，c取从1到9的自然数，
∴0≤a+b+c≤27，
∴a+b+c中不含因数37，
∴
. |
| abc |
. |
| bca |
. |
| cab |
故这样的三位数不存在．
点评：本题考查的是完全平方数、质数、不等式的有关知识．
练习册系列答案
相关题目
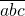（a，b，c取从1到9的自然数），使得
为完全平方数？