题目内容

是否存在一个三位数

abc

（a，b，c取从1到9的自然数），使得

abc

bca

cab

为完全平方数？

假设存在，根据题意得

abc

bca

cab

=100a+10b+c+100b+10c+a+100c+10a+b=111（a+b+c），
∵111=3×37，
而3、37是质数，
∴a+b+c的和中必有因数3和37，
又a，b，c取从1到9的自然数，
∴0≤a+b+c≤27，
∴a+b+c中不含因数37，
∴

abc

bca

cab

不是完全平方数．
故这样的三位数不存在．

练习册系列答案

相关题目

定义一种对于三位数abc（a、b、c不完全相同）的“F运算”：重排abc的三个数位上的数字，计算所得最大三位数和最小三位数的差（允许百位数字为零）．例如abc=213时，则

（1）求579经过三次“F运算”的结果（要求写出三次“F运算”的过程）；
（2）假设abc中a＞b＞c，则abc经过一次“F运算”得

99（a-c）

（用代数式表示）；
（3）若任意一个三位数经过若干次“F运算”都会得到一个固定不变的值，那么任意一个四位数也经过若干次这样的“F运算”是否会得到一个定值？若存在，请直接写出这个定值；若不存在，请说明理由．

光华中学体育组随机抽测了部分同学的身高(单位：厘米)如下：

154　　157　　158　　151.5　　158　　152.5　　158　　158　　160　　160

157　　152.5　　157　　160　　157　　162　　160　　152.5　　157　　158

(1)这部分同学的平均身高是________，中位数是________，众数是________．

(2)你求出的中位数、平均数、众数这三个指标都在抽测的数据中出现了吗？一般情况下，这三个指标中的哪几个可能不出现在所给出的原始数据中？哪几个指标是一定出现在所给出的原始数据中的？

(3)如果去掉第1个数据154，你认为平均数、众数、中位数会随之发生变化吗？如果会，将发生怎样的变化？

(4)如果增加一个数据160，你认为平均数、众数、中位数会随之发生变化吗？如果会，将发生怎样的变化？

(5)是否存在这样的数据，去掉它后不影响平均数的值？

是否存在一个三位数 $数学公式$ （a，b，c取从1到9的自然数），使得 $数学公式$ 为完全平方数？

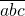是否存在一个三位数（a，b，c取从1到9的自然数），使得为完全平方数？

试题分类

是否存在一个三位数 $数学公式$ （a，b，c取从1到9的自然数），使得 $数学公式$ 为完全平方数？