题目内容
如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:
①△AED≌△AEF
②△AED为等腰三角形
③BE+DC>DE
④BE2+DC2=DE2 ,
其中正确结论的个数是( )

A.1 B.2 C.3 D.4
C
【解析】
试题分析::①∵∠DAF=90°,∠DAE=45°,∴∠FAE=∠DAF-∠DAE=45°.在△AED与△AEF中,AD=AF,∠DAE=∠FAE=45°,AE=AE,∴△AED≌△AEF(SAS),①正确;②∵∠BAC=90°,AB=AC,∴∠ABE=∠C=45°.∵点D、E为BC边上的两点,∠DAE=45°,∴AD与AE不一定相等,②错误;③∵∠BAC=∠DAF=90°,∴∠BAC-∠BAD=∠DAF-∠BAD,即∠CAD=∠BAF.在△ACD与△ABF中,AC=AB,∠CAD=∠BAF,AD=AF,∴△ACD≌△ABF(SAS),∴CD=BF,由①知△AED≌△AEF,∴DE=EF.在△BEF中,∵BE+BF>EF,∴BE+DC>DE,③正确;④由③知△ACD≌△ABF,∴∠C=∠ABF=45°,∵∠ABE=45°,∴∠EBF=∠ABE+∠ABF=90°.在Rt△BEF中,由勾股定理,得 ,∵BF=DC,EF=DE,∴
,∵BF=DC,EF=DE,∴ ,④正确.所以正确的结论有①③④.故选C.
,④正确.所以正确的结论有①③④.故选C.
考点:1.等腰直角直角三角形的性质;2.全等三角形的判定与性质;3.勾股定理.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 图象上的概率.
图象上的概率.
 ,其中
,其中
 的系数是 ,次数是 。
的系数是 ,次数是 。 时,下列函数:①
时,下列函数:① ;②
;② ;③
;③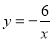 ;④
;④ ,函数值
,函数值 随自变量
随自变量 增大而增大的有( )
增大而增大的有( )