题目内容
小李想用篱笆围成一个周长为60米的矩形场地,矩形面积S(单位:平方米)随矩形一边长x(单位:米)的变化而变化.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x是多少时,矩形场地面积S最大,最大面积是多少?
(1)、S=x(30﹣x)(0<x<30);(2)、x=15时,S有最大值为225平方米. 【解析】试题分析:(1)、已知周长为60米,一边长为x,则另一边长为30﹣x.(2)、用配方法化简函数解析式,求出s的最大值. 试题解析:(1)、S=x(30﹣x) 自变量x的取值范围为: 0<x<30. (2)、S=x(30﹣x) =﹣(x﹣15)2+225, ∴当x=15时,S有最大值...
练习册系列答案
相关题目


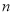 次移动结果这个点在数轴上表示的数为 ;
次移动结果这个点在数轴上表示的数为 ;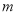 次移动后这个点在数轴上表示的数为56,求
次移动后这个点在数轴上表示的数为56,求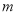 的值.
的值.
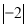 等于( )
等于( )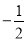 C. 2 D.
C. 2 D. 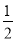
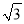 ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为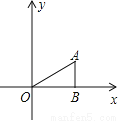
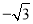 ) B. (﹣1,
) B. (﹣1, 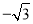 )或(﹣2,0) C. (
)或(﹣2,0) C. (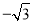 ,﹣1)或(0,﹣2) D. (
,﹣1)或(0,﹣2) D. (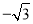 ,﹣1)
,﹣1)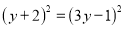 (分解因式法) (4)x2-4x-396=0(适当的方法)
(分解因式法) (4)x2-4x-396=0(适当的方法) x (D)y=
x (D)y= x
x