题目内容
如图，在菱形ABCD中，E为AD中点，EF⊥AC交CB的延长线于F．求证：AB与EF互相平分．
连接BD，AF，BE，
在菱形ABCD中，AC⊥BD
∵EF⊥AC，
∴EF∥BD，又ED∥FB，
∴四边形EDBF是平行四边形，DE=BF，
∵E为AD的中点，
∴AE=ED，∴AE=BF，
又AE∥BF，
∴四边形AEBF为平行四边形，
即AB与EF互相平分．
【解析】
试题分析：由菱形的性质可证AC⊥BD，又已知EF⊥AC，所以AG=BG，GE=
BD，AD∥BC，可证四边形EDBF为平行四边形，可证GE=GF，即证结论．
试题解析：连接BD，AF，BE，
在菱形ABCD中，AC⊥BD
∵EF⊥AC，
∴EF∥BD，又ED∥FB，
∴四边形EDBF是平行四边形，DE=BF，
∵E为AD的中点，
∴AE=ED，∴AE=BF，
又AE∥BF，
∴四边形AEBF为平行四边形，
即AB与EF互相平分．
【难度】一般
练习册系列答案
相关题目
图象上的点是 （ ） 
ABCD，如图1和图2．现有1号、2号两游览车分别从出口A和景点C同时出发，1号车顺时针、2号车逆时针沿环形路连续循环行驶．供游客随时免费乘车（上、下车的时间忽略不计），两车速度均为200米／分．
：
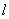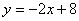分别与
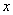轴、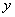
轴交于A、B两点，点C线段AB上，作CD⊥x轴于D, CD=2OD, 点E线段OB上,且AE=BE；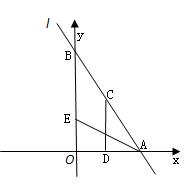
过点E，且将△AOB分成面积比为1：2的两部分，求直线
－
；
”．一元二次方程x2－x－2＝0可通过因式分解化为（x－2）（x＋1）＝0，由基本事实得x－2＝0或x＋1＝0，即方程的解为x＝2或x＝－1．
－1）－2＝0，求x2＋y2的值．
．
的结果是 ．