题目内容
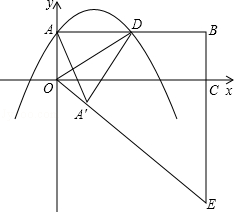
如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在y轴和x轴的正半轴上,且长分别为m、4m(m>0),D为边AB的中点,一抛物线l经过点A、D及点M(﹣1,﹣1﹣m).
(1)求抛物线l的解析式(用含m的式子表示);
(2)把△OAD沿直线OD折叠后点A落在点A′处,连接OA′并延长与线段BC的延长线交于点E,若抛物线l与线段CE相交,求实数m的取值范围;
(3)在满足(2)的条件下,求出抛物线l顶点P到达最高位置时的坐标.

(1)求抛物线l的解析式(用含m的式子表示);
(2)把△OAD沿直线OD折叠后点A落在点A′处,连接OA′并延长与线段BC的延长线交于点E,若抛物线l与线段CE相交,求实数m的取值范围;
(3)在满足(2)的条件下,求出抛物线l顶点P到达最高位置时的坐标.
解:(1)设抛物线l的解析式为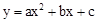 ,
,
将A(0,m),D(2m,m),M(﹣1,﹣1﹣m)三点的坐标代入,得
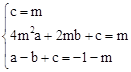 ,解得
,解得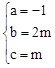 。
。
∴抛物线l的解析式为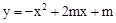 。
。
(2)设AD与x轴交于点M,过点A′作A′N⊥x轴于点N,
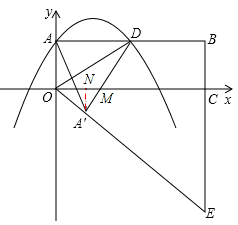
∵把△OAD沿直线OD折叠后点A落在点A′处,
∴△OAD≌△OA′D,OA=OA′=m,AD=A′D=2m,∠OAD=∠OA′D=90°,∠ADO=∠A′DO。
∵矩形OABC中,AD∥OC,∴∠ADO=∠DOM。
∴∠A′DO=∠DOM。∴DM=OM。
设DM=OM=x,则A′M=2m﹣x,
在Rt△OA′M中,∵OA′2+A′M2=OM2,
∴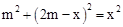 ,解得
,解得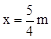 。
。
∵ ,∴
,∴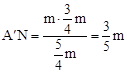 。
。
∴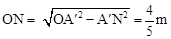 。
。
∴A′点坐标为(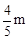 ,
,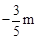 )。
)。
易求直线OA′的解析式为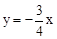 ,
,
当x=4m时,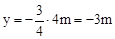 ,∴E点坐标为(4m,
,∴E点坐标为(4m,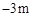 )。
)。
当x=4m时,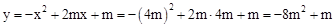 ,
,
∴抛物线l与直线CE的交点为(4m,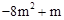 )。
)。
∵抛物线l与线段CE相交,∴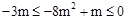 。
。
∵m>0,∴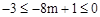 ,解得
,解得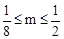 。
。
(3)∵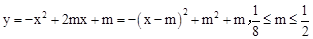 ,
,
∴当x=m时,y有最大值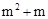 。
。
又∵ ,
,
∴当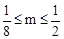 时,
时,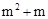 随m的增大而增大。
随m的增大而增大。
∴当m=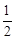 时,顶点P到达最高位置,
时,顶点P到达最高位置,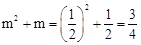 。
。
∴此时抛物线l顶点P到达最高位置时的坐标为(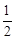 ,
,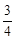 )
)
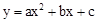 ,
,将A(0,m),D(2m,m),M(﹣1,﹣1﹣m)三点的坐标代入,得
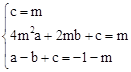 ,解得
,解得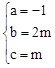 。
。∴抛物线l的解析式为
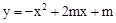 。
。(2)设AD与x轴交于点M,过点A′作A′N⊥x轴于点N,

∵把△OAD沿直线OD折叠后点A落在点A′处,
∴△OAD≌△OA′D,OA=OA′=m,AD=A′D=2m,∠OAD=∠OA′D=90°,∠ADO=∠A′DO。
∵矩形OABC中,AD∥OC,∴∠ADO=∠DOM。
∴∠A′DO=∠DOM。∴DM=OM。
设DM=OM=x,则A′M=2m﹣x,
在Rt△OA′M中,∵OA′2+A′M2=OM2,
∴
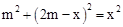 ,解得
,解得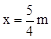 。
。∵
 ,∴
,∴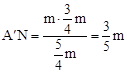 。
。∴
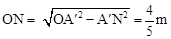 。
。∴A′点坐标为(
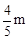 ,
,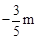 )。
)。易求直线OA′的解析式为
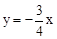 ,
,当x=4m时,
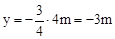 ,∴E点坐标为(4m,
,∴E点坐标为(4m,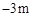 )。
)。当x=4m时,
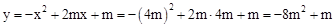 ,
,∴抛物线l与直线CE的交点为(4m,
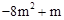 )。
)。∵抛物线l与线段CE相交,∴
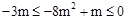 。
。∵m>0,∴
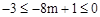 ,解得
,解得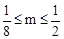 。
。(3)∵
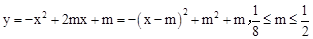 ,
,∴当x=m时,y有最大值
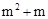 。
。又∵
 ,
,∴当
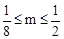 时,
时,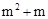 随m的增大而增大。
随m的增大而增大。∴当m=
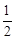 时,顶点P到达最高位置,
时,顶点P到达最高位置,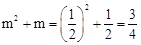 。
。∴此时抛物线l顶点P到达最高位置时的坐标为(
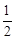 ,
,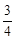 )
)试题分析:(1)设抛物线l的解析式为
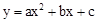 ,将A、D、M三点的坐标代入,运用待定系数法即可求解。
,将A、D、M三点的坐标代入,运用待定系数法即可求解。(2)设AD与x轴交于点M,过点A′作A′N⊥x轴于点N.根据轴对称及平行线的性质得出DM=OM=x,则A′M=2m﹣x,OA′=m,在Rt△OA′M中运用勾股定理求出x,得出A′点坐标,运用待定系数法得到直线OA′的解析式,确定E点坐标(4m,﹣3m),根据抛物线l与线段CE相交,列出关于m的不等式组,求出解集即可。
(3)根据二次函数的性质,结合(2)中求出的实数m的取值范围,即可求解。

练习册系列答案
相关题目
 上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为
上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为




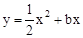 与直线
与直线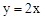 交于点O(0,0),
交于点O(0,0),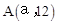 。点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E。
。点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E。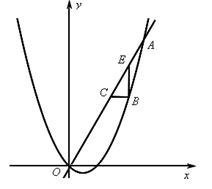
 交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法:
交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法: 时,BP2=BO•BA;
时,BP2=BO•BA; .
. 与x轴的交点个数为
与x轴的交点个数为  与
与 轴的交点的个数是___________.
轴的交点的个数是___________. (a≠0)的图象如图所示,则下列结论中正确的是
(a≠0)的图象如图所示,则下列结论中正确的是
 ,同理
,同理 ,所以AB的中点坐标为
,所以AB的中点坐标为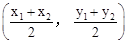 .由勾股定理得
.由勾股定理得 ,所以A、B两点间的距离公式为
,所以A、B两点间的距离公式为 .
.
 的顶点坐标是 .
的顶点坐标是 .