题目内容
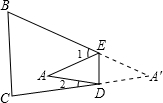
 如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE外部点A'的位置,则∠A'、∠1与∠2的数量关系,结论正确的是
如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE外部点A'的位置,则∠A'、∠1与∠2的数量关系,结论正确的是
- A.∠1=∠2+∠A′
- B.∠1=2∠2+2∠A′
- C.2∠1=∠2+∠A′
- D.∠1=2∠A′+∠2
D
分析:先根据图形翻折变换的性质得出∠A=∠A′,再根据三角形外角的性质进行解答即可.
解答: 解:∵△A′ED是△AED翻折变换而成,
解:∵△A′ED是△AED翻折变换而成,
∴∠A=∠A′,
∵∠AFE是△A′DF的外角,
∴∠AFE=∠A′+∠2,
∵∠1是△AEF的外角,
∴∠1=∠A+∠AFE,即∠1=∠A+∠A′+∠2=2∠A′+∠2.
故选D.
点评:本题考查的是图形翻折变换的性质及三角形外角的性质,熟知以上知识是解答此题的关键.
分析:先根据图形翻折变换的性质得出∠A=∠A′,再根据三角形外角的性质进行解答即可.
解答:
 解:∵△A′ED是△AED翻折变换而成,
解:∵△A′ED是△AED翻折变换而成,∴∠A=∠A′,
∵∠AFE是△A′DF的外角,
∴∠AFE=∠A′+∠2,
∵∠1是△AEF的外角,
∴∠1=∠A+∠AFE,即∠1=∠A+∠A′+∠2=2∠A′+∠2.
故选D.
点评:本题考查的是图形翻折变换的性质及三角形外角的性质,熟知以上知识是解答此题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,

 20、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,∠A与∠1、∠2之间存在一种始终保持不变的数量关系,这个数量关系是
20、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,∠A与∠1、∠2之间存在一种始终保持不变的数量关系,这个数量关系是 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,