Question

已知抛物线y＝ax²＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．

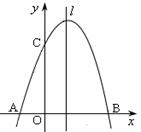(1)求抛物线的解析式和对称轴；      

(2)设点P是直线l上的一个动点，当△PAC是以AC为斜边的Rt△时，求点P的坐标；

(3)在直线l上是否存在点M，使△MAC为等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由；

(4)设过点A的直线与抛物线在第一象限的交点为N，当△ACN的面积为时，求直线AN的解析式.

Answer 1

解：（1）设抛物线解析式为：

对称轴为：直线

（注：对称轴未写直线二字不扣分）

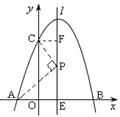（2）设点P（1，y）是直线l上的一个动点，作CF⊥l于F，l交x轴于E，

则AC²＝AO²＋CO²＝10，CP²＝CF²＋PF²＝1＋（3－y）²＝

AP²＝AE²＋PE²＝4＋y², ∴由CP²＋AP²＝AC²，

得：＋4＋y²＝10，解得或

∴P点的坐标为P₁（1，1）、P₂（1, 2）

（说明: 求得一个点1分、2个点3分，求解过程不必要求过细，看结果为主）

（解法二 用△相似解法更简单如下：

∵CP⊥AP，∴△CPF∽△PAE，∴，∴∴解得或 同样给分）

（3）设点M（1，m）, 与（2）同理可得：AC²＝10，CM²＝，AM²＝4＋m²

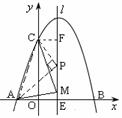①当AC＝CM时，10＝，解得：m＝0或m＝6（舍去）

②当AC＝AM时，10＝4＋m², 解得：m＝或m＝

③当CM＝AM时，＝4＋m²，解得：m＝1

检验：当m＝6时，M、A、C三点共线，不合题意，故舍去；

综上可知，符合条件的M点有4个，

M坐标为(1，0) 、(1，)、(1，－)、(1，1)

（注：求出5个点，未舍去(1，6)，不扣分）

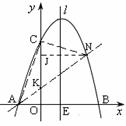
(4) 设直线AN的解析式为，且交y轴于点K，∵过点A（—1, 0），∴，

∴K（0，k），∵N是直线AN与抛物线的交点，∴，解得x＝3—k，

或x＝—1（舍去），∴N点的横坐标为x＝3—k （k＜3）  

由S_△ACN＝S_△ACK＋S_△CKN＝CK·OA＋CK·NJ＝（3—k）×1＋（3—k）²

＝ 令＝，解得k＝（舍去），或k＝，

∴直线AN的解析式为