题目内容
10.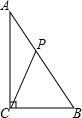 如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动,在运动过程中,当△APC为等腰三角形时,点P出发的时间t可能的值为4或$\frac{5}{2}$.
如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动,在运动过程中,当△APC为等腰三角形时,点P出发的时间t可能的值为4或$\frac{5}{2}$.
分析 没有指明等腰三角形的底边,所以需要分类讨论:AP=AC,AP=PC,AC=PC.
解答  解:如图,∵在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,
解:如图,∵在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,
∴由勾股定理,得BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=6cm.
①当AP=AC时,2t=8,则t=4;
②当AP=PC时,过点P作PD⊥AC于点D,则AD=CD,PD∥BC,
∴PD是△ABC的中位线,
∴点P是AB的中点,
∴2t=5,即t=$\frac{5}{2}$;
③若AC=PC=8cm时,与PC<AC矛盾,不符合题意.
综上所述,t的值是4或$\frac{5}{2}$.
故答案为:4或$\frac{5}{2}$.
点评 本题考查了勾股定理,等腰三角形的判定和性质,注意要分类讨论,还要注意PC的取值范围.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
20.⊙O的半径r=5cm,点P在直线l上,若OP=6cm,则直线l与⊙O的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 不能确定 |
15.一个长方体的体积为x2-2xy+x,高是x,则这个长方体的底面积是( )
| A. | x-2y | B. | x+2y | C. | x-2y-1 | D. | x-2y+l |
 如图,过反比例函数y=$\frac{6}{x}$(x>0)图象上一点A作x轴的平行线,交双曲线y=-$\frac{3}{x}$(x<0)于点B,过B作BC∥OA交双曲线y=-$\frac{3}{x}$(x<0)于点D,交x轴于点C,连接AD交y轴于点E.若OC=3,求OE的长.
如图,过反比例函数y=$\frac{6}{x}$(x>0)图象上一点A作x轴的平行线,交双曲线y=-$\frac{3}{x}$(x<0)于点B,过B作BC∥OA交双曲线y=-$\frac{3}{x}$(x<0)于点D,交x轴于点C,连接AD交y轴于点E.若OC=3,求OE的长. 如图,已知∠B+∠D+∠BED=360°,那么AB与CD有怎样的位置关系,请说明理由.
如图,已知∠B+∠D+∠BED=360°,那么AB与CD有怎样的位置关系,请说明理由.