Question

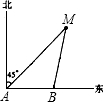上午9时，一条船从A处出发，以每小时40海里的速度向正东方向航行，9时30分到达B处（如图）．从A、B两处分别测得小岛M在北偏东45°和北偏东15°方向，那么在B处船与小岛M的距离为（　　）

• A、20海里
• B、20

  2

  海里
• C、15

  3

  海里
• D、20

  3

  海里

Answer 1

分析：过点B作BN⊥AM于点N．根据三角函数求BN的长，从而求BM的长．

解答：解：如图，过点B作BN⊥AM于点N．
由题意得，AB=40×

1

2

=20海里，∠ABM=105°．
作BN⊥AM于点N．
在直角三角形ABN中，BN=AB•sin45°=10

2

．
在直角△BNM中，∠MBN=60°，则∠M=30°，
所以BM=2BN=20

2

（海里）．
故选B．

点评：解一般三角形，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．