题目内容
19.已知在直角坐标系中,一条直线经过点A(-1,5),P(-2,a),B(3,-3)三点.(1)求直线表达式,并请你判断点(-$\frac{1}{2}$,-2)是否在此函数图象上;
(2)求a的值;
(3)设这条直线与y轴相交于点D,求△OPD的面积.
分析 (1)设直线的表达式为y=kx+b,把点A、B的坐标代入求出k、b,即可得出答案;
(2)把P点的坐标代入求出即可;
(3)画出图象,求出D点的坐标,根据坐标和三角形面积公式求出即可.
解答 解:(1)设直线的表达式为y=kx+b,
把点A、B的坐标代入得:$\left\{\begin{array}{l}{-k+b=5}\\{3k+b=-3}\end{array}\right.$,
解得:k=-2,b=3,
所以直线表达式解析式为y=-2x+3,
把点(-$\frac{1}{2}$,-2)代入得:左边=-2,右边=4,
左边≠右边,
所以点(-$\frac{1}{2}$,-2)不在此函数图象上;
(2)把P(-2,a)代入y=-2x+3得:a=7;
(3)
∵把x=0代入y=-2x+3得:y=3,
∴直线y=-2x+3与y轴的交点为(0,3),
即OD=3,
∵P(-2,7),
∴△OPD的面积为$\frac{1}{2}$×3×|-2|=3.
点评 本题考查了用待定系数法求一次函数的解析式,一次函数图象上点的坐标特征的应用,能综合运用知识点进行求值是解此题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
10.五一期间,绿化部门预在县城主要干道旁边种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵,求A、B两种花木的数量分别是多少棵?若设A,B花木各x棵,y棵,则有( )
| A. | $\left\{\begin{array}{l}{x+y=6600}\\{x=2y+600}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=6600}\\{y=2x+600}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=6600}\\{y=2x-600}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=6600}\\{x=2y-600}\end{array}\right.$ |
4. 如图,直线a∥b,∠1=37°,则∠2的度数是( )
如图,直线a∥b,∠1=37°,则∠2的度数是( )
 如图,直线a∥b,∠1=37°,则∠2的度数是( )
如图,直线a∥b,∠1=37°,则∠2的度数是( )| A. | 57° | B. | 37° | C. | 143° | D. | 53° |
11. 如图,直线a,b,c相交于点A,直线c,d,e相交于点B,则图中属于内错角的是( )
如图,直线a,b,c相交于点A,直线c,d,e相交于点B,则图中属于内错角的是( )
 如图,直线a,b,c相交于点A,直线c,d,e相交于点B,则图中属于内错角的是( )
如图,直线a,b,c相交于点A,直线c,d,e相交于点B,则图中属于内错角的是( )| A. | ∠1和∠2 | B. | ∠2和∠3 | C. | ∠1和∠3 | D. | ∠3和∠4 |
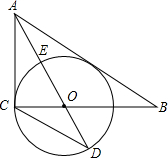 如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O. 如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,连接BE、AD交于点P,求证:
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,连接BE、AD交于点P,求证: 如图,在矩形ABCD中,$\frac{AB}{BC}=\frac{3}{5}$,AC为对角线,BM⊥AC于点M,交AD于点N,点O是BC边上一点,$\frac{OC}{BC}=\frac{1}{3}$,连接DO交AC于点P,OF⊥OD交BN于点E,交AB边于点F.
如图,在矩形ABCD中,$\frac{AB}{BC}=\frac{3}{5}$,AC为对角线,BM⊥AC于点M,交AD于点N,点O是BC边上一点,$\frac{OC}{BC}=\frac{1}{3}$,连接DO交AC于点P,OF⊥OD交BN于点E,交AB边于点F.