题目内容
7.解下列方程组或不等式组:(1)$\left\{\begin{array}{l}{2x+y=5}\\{x-3y=6}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x-3(x-1)≤7}\\{1-\frac{2-5x}{3}>x}\end{array}\right.$.
分析 (1)利用代入消元法求解即可;
(2)先求出两个不等式的解集,再求其公共解.
解答 解:(1)$\left\{\begin{array}{l}{2x+y=5①}\\{x-3y=6②}\end{array}\right.$,
由②得,x=6+3y③,
把③代入①得,12+6y+y=5,
解得y=-1,
把y=-1代入③得,x=6+3×(-1),
解得x=3,
所以,方程组的解是$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x-3(x-1)≤7①}\\{1-\frac{2-5x}{3}>x②}\end{array}\right.$,
由①得,x≥2,
由②得,x$>-\frac{1}{2}$,
所以,不等式组的解集是x≥2.
点评 本题主要考查了代入法解二元一次方程组以及一元一次不等式组解集的求法,求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).

练习册系列答案
相关题目
18.下列方程中,有实数根的是( )
| A. | x2+1=0 | B. | x2+x+1=0 | C. | x2-x-1=0 | D. | x2-x+1=0 |
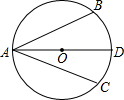 如图,AD为⊙O的直径,AB、AC为弦,且AD平分∠BAC,试判定AB与AC的关系,并证明你的结论.
如图,AD为⊙O的直径,AB、AC为弦,且AD平分∠BAC,试判定AB与AC的关系,并证明你的结论. 如图,直线a∥b,∠1=53°,那么∠2=127°.
如图,直线a∥b,∠1=53°,那么∠2=127°. 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$,在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点.若四边形BEDF的面积为6,则k的值为( )
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$,在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点.若四边形BEDF的面积为6,则k的值为( )