题目内容
在圆内接四边形ABCD中,若∠A:∠B:∠C=2:3:6,则∠D等于
- A.67.5°
- B.135°
- C.112.5°
- D.45°
C
分析:根据四边形ABCD是⊙O的内接四边形,得出∠A+∠C=180°,∠B+∠D=180°,设∠A=2a,∠B=3a,∠C=6a,得出2a+6a=180°,求出a的值,求出∠B的度数,即可求出答案.
解答:
∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠C=180°,∠B+∠D=180°,
∵∠A:∠B:∠C=2:3:6,
设∠A=2a,∠B=3a,∠C=6a,
则2a+6a=180°,
∴a=22.5°,
∴∠B=3a=67.5°,
∴∠D=180°-∠B=112.5°.
故选C.
点评:本题考查了对圆内接四边形的性质的运用,关键是得出关于a的方程,题目是一道具有代表性的题目,主要培养学生的计算能力.
分析:根据四边形ABCD是⊙O的内接四边形,得出∠A+∠C=180°,∠B+∠D=180°,设∠A=2a,∠B=3a,∠C=6a,得出2a+6a=180°,求出a的值,求出∠B的度数,即可求出答案.
解答:

∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠C=180°,∠B+∠D=180°,
∵∠A:∠B:∠C=2:3:6,
设∠A=2a,∠B=3a,∠C=6a,
则2a+6a=180°,
∴a=22.5°,
∴∠B=3a=67.5°,
∴∠D=180°-∠B=112.5°.
故选C.
点评:本题考查了对圆内接四边形的性质的运用,关键是得出关于a的方程,题目是一道具有代表性的题目,主要培养学生的计算能力.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
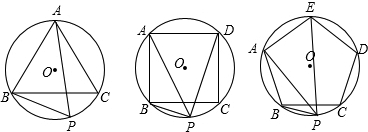

 (2013•梧州一模)如图,在圆的内接四边形ABCD中,∠ABC=120°,则四边形ABCD的外角∠ADE的度数是( )
(2013•梧州一模)如图,在圆的内接四边形ABCD中,∠ABC=120°,则四边形ABCD的外角∠ADE的度数是( )
 上一点,则PB+PC=PA;
上一点,则PB+PC=PA;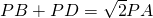 ;
;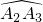 上一点,请问PA2+PAn与PA1又有怎样的数量关系,写出结论,不要求证明.
上一点,请问PA2+PAn与PA1又有怎样的数量关系,写出结论,不要求证明.
 上一点,则PB+PC=PA;
上一点,则PB+PC=PA; 上一点,则
上一点,则 ;
; 上一点,请问PB+PE与PA有怎样的数量关系,写出结论,并加以证明;
上一点,请问PB+PE与PA有怎样的数量关系,写出结论,并加以证明; 上一点,请问PA2+PAn与PA1又有怎样的数量关系,写出结论,不要求证明.
上一点,请问PA2+PAn与PA1又有怎样的数量关系,写出结论,不要求证明.