题目内容
 若菱形ABCD的周长为16,∠A:∠B=1:2,则菱形的面积为( )
若菱形ABCD的周长为16,∠A:∠B=1:2,则菱形的面积为( )A、2
| ||
B、3
| ||
C、4
| ||
D、8
|
分析:根据邻角互补可得出∠ABC=60°,∠BAC=120°,从而根据菱形的对角线互相垂直且平分的性质可分别求出两对角线的长,进而根据菱形的面积等于对角线乘积的一半进行解答.
解答:解:∵菱形ABCD的周长为16,
∴AB=BC=CD=DA=4,
又∵∠A:∠B=1:2,
∴∠ABC=60°,∠BAC=120°,
∴∠AB0=
∠ABC=30°,
在Rt△ABO中,
AO=
AB=2,BO=
AB=2
,
∴AC=4,BD=4
,
∴菱形的面积=
AC×BD=8
.
故选D.
∴AB=BC=CD=DA=4,
又∵∠A:∠B=1:2,
∴∠ABC=60°,∠BAC=120°,
∴∠AB0=
| 1 |
| 2 |
在Rt△ABO中,
AO=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴AC=4,BD=4
| 3 |
∴菱形的面积=
| 1 |
| 2 |
| 3 |
故选D.
点评:本题考查了菱形的性质,属于基础题,解答本题用到的知识点为:①菱形的四边形等,菱形的对角线互相垂直且平分,②菱形的面积等于对角线乘积的一半.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 如图,在菱形ABCD中,对角线AC、BD交于点O,H为AD边的中点.若菱形ABCD的周长为32,则OH的长为
如图,在菱形ABCD中,对角线AC、BD交于点O,H为AD边的中点.若菱形ABCD的周长为32,则OH的长为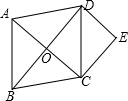 如图,O是菱形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE,CE交于点E.
如图,O是菱形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE,CE交于点E. (2013•宝安区一模)已知矩形BEDG和矩形BNDQ中,BE=BN,DE=DN.
(2013•宝安区一模)已知矩形BEDG和矩形BNDQ中,BE=BN,DE=DN.