题目内容
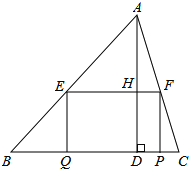
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,高
,高![]() , 矩形
, 矩形![]() 的一边
的一边![]() 在
在![]() 边上,
边上,![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)设![]() ,当
,当![]() 为何值时,矩形
为何值时,矩形![]() 的面积最大?并求出最大面积;
的面积最大?并求出最大面积;
(3)当矩形![]() 的面积最大时,该矩形
的面积最大时,该矩形![]() 以每秒
以每秒![]() 个单位的速度沿射线
个单位的速度沿射线![]() 匀速向上运动(当矩形的边
匀速向上运动(当矩形的边![]() 到达
到达![]() 点时停止运动),设运动时间为
点时停止运动),设运动时间为![]() 秒,矩形
秒,矩形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)当x为![]() 时,矩形的面积有最大值5;(3)S=
时,矩形的面积有最大值5;(3)S=
【解析】
(1)由条件可得EF∥BC,根据相似三角形的判定即可求证;
(2)由(1)可得![]() ,用x表示出HD,表示出矩形EFPQ的面积,利用二次函数可求得其最大值;
,用x表示出HD,表示出矩形EFPQ的面积,利用二次函数可求得其最大值;
(3)当0≤t<2时,设矩形EFPQ与AB、AC的交点分别为M、N、R、S,可利用平行表示出MN的长,可表示出△EMS和△NFR的面积,进一步可表示出重叠部分的面积;当2≤t≤4时,重叠部分为△P′Q′A,利用平行分别用x表示出其底和高,可表示出面积.
解:(1)∵四边形EFPQ为矩形,
∴EF∥BC,
∴![]() ;
;
(2)∵![]()
∴![]() ,即
,即![]() ,
,
∴HD=4-![]() ,
,
∴S矩形EFPQ=EFFQ=EFHD=x(4-![]() )=-
)=-![]() x2+4x,
x2+4x,
该函数为开口向下的二次函数,故当x=![]() 时有最大值,最大值为5,
时有最大值,最大值为5,
即当x为![]() 时,矩形的面积有最大值5;
时,矩形的面积有最大值5;
(3)由(2)可知,当矩形面积取最大值时,EF=![]() ,FQ=2,
,FQ=2,
①当0≤t≤2时,如图1,设矩形与AB、AC分别交与点M、N、R、S,与AD交于J、L,连接RS,交AD于K,
由题意可知LD=JK=t,则AJ=AD-LD-JL=4-t-2=2-t,
又∵RS=![]() ,
,
∴R、S为AB、AC的中点,
∴AK=![]() AD=2,ES=FR=JK=t,
AD=2,ES=FR=JK=t,
又∵MN∥RS,
∴![]() ,即
,即 ,
,
∴![]() -
-![]() t,
t,
∴EM+FN=EF-MN=![]() -(
-(![]() -
-![]() t)=
t)=![]() t,
t,
∴S△EMS+S△FNR=![]() ES(EM+FN)=
ES(EM+FN)=![]() t
t![]() t=
t=![]() ,
,
∴S=S矩形EFPQ-(S△EMS+S△FNR)=5-![]() ;
;
②当2<t≤4时,如图2,设矩形与AB、AC、AD分别交于点Q′、P′、D′,
根据题意D′D=t,则AD′=4-t,
∵PQ∥BC,
∴![]() ,即
,即![]() ,
,
解得P′Q′=5-![]() t,
t,
∴S=S△AP′Q′=![]() P′Q′AD′=
P′Q′AD′=![]() (4-t)(5-
(4-t)(5-![]() t)=
t)=![]() -5t+10;
-5t+10;
综上可知S= .
.

 阅读快车系列答案
阅读快车系列答案