题目内容
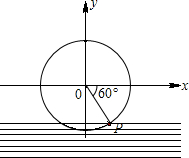 如图,半径为4m的水车圆O放在坐标系xOy中,已知水车每分钟按逆时针方向转1圈,如果水车上点P从浮出水时开始计算时间,此时OP与x轴正方向夹角为60°,则当水车转15秒时,点P上升的高度为
如图,半径为4m的水车圆O放在坐标系xOy中,已知水车每分钟按逆时针方向转1圈,如果水车上点P从浮出水时开始计算时间,此时OP与x轴正方向夹角为60°,则当水车转15秒时,点P上升的高度为分析:首先确定水车转15秒时到达A处,然后计算∠POA的度数,从而得到∠AOB的度数,再过A作AB⊥x轴,过P作PC⊥x轴,利用直角三角形30°角所对的边是斜边的一半得到AB=2,再运用三角函数计算PC的长,就可以得到点P上升的高度.
解答: 解:当水车转15秒时到达A处,过A作AB⊥x轴,过P作PC⊥x轴,
解:当水车转15秒时到达A处,过A作AB⊥x轴,过P作PC⊥x轴,
∵水车每分钟按逆时针方向转1圈,
∴当水车转15秒时∠POA=90°,
∵∠POB=60°,
∴∠AOB=30°,
∵OA=4m,
∴AB=
OA=2m,
∵OP=4m,∠POB=60°,
∴OC=OP•sin60°=4m•
=2
m,
∴AB+PC=2+2
.
故填:2+2
.
 解:当水车转15秒时到达A处,过A作AB⊥x轴,过P作PC⊥x轴,
解:当水车转15秒时到达A处,过A作AB⊥x轴,过P作PC⊥x轴,∵水车每分钟按逆时针方向转1圈,
∴当水车转15秒时∠POA=90°,
∵∠POB=60°,
∴∠AOB=30°,
∵OA=4m,
∴AB=
| 1 |
| 2 |
∵OP=4m,∠POB=60°,
∴OC=OP•sin60°=4m•
| ||
| 2 |
| 3 |
∴AB+PC=2+2
| 3 |
故填:2+2
| 3 |
点评:此题主要考查了勾股定理与三角函数的综合应用.

练习册系列答案
相关题目

 m.
m. ),求圆形喷水池的半径.
),求圆形喷水池的半径.
 如图,半径为4m的水车圆O放在坐标系xOy中,已知水车每分钟按逆时针方向转1圈,如果水车上点P从浮出水时开始计算时间,此时OP与x轴正方向夹角为60°,则当水车转15秒时,点P上升的高度为________.
如图,半径为4m的水车圆O放在坐标系xOy中,已知水车每分钟按逆时针方向转1圈,如果水车上点P从浮出水时开始计算时间,此时OP与x轴正方向夹角为60°,则当水车转15秒时,点P上升的高度为________.