题目内容
已知抛物线经过点A(0,4)、B(1,4)、C(3,2),与x轴正半轴交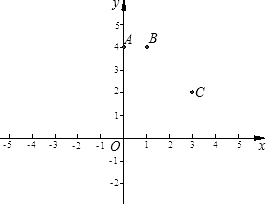 于点D.
于点D.(1)求此抛物线的解析式及点D的坐标;
(2)在x轴上求一点E,使得△BCE是以BC为底边的等腰三角形;
(3)在(2)的条件下,过线段ED上动点P作直线PF∥BC,与BE、CE分别交于点F、G,将△EFG沿FG翻折得到△E′FG.设P(x,0),△E′FG与四边形FGCB重叠部分的面积为S,求S与x的函数关系式及自变量x的取值范围.
分析:(1)根据抛物线经过点A(0,4)、B(1,4)、C(3,2),于是可设出一般式,用待定系数法求出解析式,再根据解析式求出D点坐标;
(2)设出E点坐标,作出辅助直角三角形,运用等腰三角形的性质和勾股定理建立等式,求出E点坐标;
(3)由于P点为动点,故根据x的不同取值会得到不同的重叠图形.由于BC的中点横坐标为
=2,抛物线与x轴的交点横坐标4,所以分-1<x≤2,2<x≤4等情况讨论.
(2)设出E点坐标,作出辅助直角三角形,运用等腰三角形的性质和勾股定理建立等式,求出E点坐标;
(3)由于P点为动点,故根据x的不同取值会得到不同的重叠图形.由于BC的中点横坐标为
| 1+3 |
| 2 |
解答: 解:(1)依题意,设所求抛物线的解析式为y=ax2+bx+4,
解:(1)依题意,设所求抛物线的解析式为y=ax2+bx+4,
则
,(1分)
解得
,
∴所求抛物线的解析式为y=-
x2+
x+4.(2分)
由-
x2+
x+4=0,
解得x1=4,x2=-3.
∴D(4,0).(3分)
(2)如图,过点C作CN⊥x轴于N,过点E、B分别
作x轴、y轴的垂线,两线交于点M.
∴∠M=∠CNE=90度.
设E(a,0),EB=EC.
∴BM2+EM2=CN2+EN2.
∴(1-a)2+(4-0)2=(2-0)2+(3-a)2.
解得a=-1.
∴E(-1,0).(4分)
(3)可求得直线BC的解析式为y=-x+5.
从而直线BC与x轴的交点为H(5,0).
如图,根据轴对称性可知S△E′FG=S△EFG,
当点E′在BC上时,点F是BE的中点.
∵FG∥BC,
∴△EFP∽△EBH.
可证EP=PH.
∵E(-1,0),H(5,0),
∴P(2,0).(5分)
(i)如图,分别过点B、C作BK⊥ED于K,
CJ⊥ED于J,
则S△BCE=S△BEH-S△CEH=
EH•(BK-CJ)=6.
当-1<x≤2时,
∵PF∥BC,
∴△EGP∽△ECH,△EFG∽△EBC.
∴
=
,
=
=
∵P(x,0),E(-1,0),H(5,0),
∴EP=x+1,EH=6.
∴S=S△E′FG=S△EFG=
=
x2+
x+
(-1<x≤2).(6分)
(ii)如图,当2<x≤4时,在x轴上截取一点Q,使得PQ=HP,过点Q作
QM∥FG,分别交EB、EC于M、N.
可证S=S四边形MNGF,△ENQ∽△ECH,△EMN∽△EBC.
∴
=
,
=
=
∵P(x,0),E(-1,0),H(5,0),
∴EH=6,PQ=PH=5-x,EP=x+1,
EQ=6-2(5-x)=2x-4.
∴S△EMN=
(7分)
同(i)可得S△EFG=
,
∴S=S△EFG-S△EMN=
-
=-
x2+3x-
(2<x≤4).(8分)
综上,S=
.
 解:(1)依题意,设所求抛物线的解析式为y=ax2+bx+4,
解:(1)依题意,设所求抛物线的解析式为y=ax2+bx+4,则
|
解得
|
∴所求抛物线的解析式为y=-
| 1 |
| 3 |
| 1 |
| 3 |
由-
| 1 |
| 3 |
| 1 |
| 3 |
解得x1=4,x2=-3.
∴D(4,0).(3分)
(2)如图,过点C作CN⊥x轴于N,过点E、B分别
作x轴、y轴的垂线,两线交于点M.
∴∠M=∠CNE=90度.
设E(a,0),EB=EC.
∴BM2+EM2=CN2+EN2.
∴(1-a)2+(4-0)2=(2-0)2+(3-a)2.
解得a=-1.
∴E(-1,0).(4分)
(3)可求得直线BC的解析式为y=-x+5.

从而直线BC与x轴的交点为H(5,0).
如图,根据轴对称性可知S△E′FG=S△EFG,
当点E′在BC上时,点F是BE的中点.
∵FG∥BC,
∴△EFP∽△EBH.
可证EP=PH.
∵E(-1,0),H(5,0),
∴P(2,0).(5分)
(i)如图,分别过点B、C作BK⊥ED于K,
CJ⊥ED于J,
则S△BCE=S△BEH-S△CEH=
| 1 |
| 2 |
当-1<x≤2时,
∵PF∥BC,

∴△EGP∽△ECH,△EFG∽△EBC.
∴
| EG |
| EC |
| EP |
| EH |
| S△EFG |
| S△EBC |
| EG2 |
| EC2 |
| EP2 |
| EH2 |
∵P(x,0),E(-1,0),H(5,0),
∴EP=x+1,EH=6.
∴S=S△E′FG=S△EFG=
| (x+1)2 |
| 6 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 6 |
(ii)如图,当2<x≤4时,在x轴上截取一点Q,使得PQ=HP,过点Q作
QM∥FG,分别交EB、EC于M、N.
可证S=S四边形MNGF,△ENQ∽△ECH,△EMN∽△EBC.
∴
| EN |
| EC |
| EQ |
| EH |
| S△EFG |
| S△EBC |
| EN2 |
| EC2 |
| EQ2 |
| EH2 |
∵P(x,0),E(-1,0),H(5,0),
∴EH=6,PQ=PH=5-x,EP=x+1,

EQ=6-2(5-x)=2x-4.
∴S△EMN=
| (2x-4)2 |
| 6 |
同(i)可得S△EFG=
| (x+1)2 |
| 6 |
∴S=S△EFG-S△EMN=
| (x+1)2 |
| 6 |
| (2x-4)2 |
| 6 |
| 1 |
| 2 |
| 5 |
| 2 |
综上,S=
|
点评:此题不仅考查了用待定系数法求二次函数解析式,还结合等腰三角形的性质考查了运用勾股定理求线段的长,解(3)时要注意进行分类讨论.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
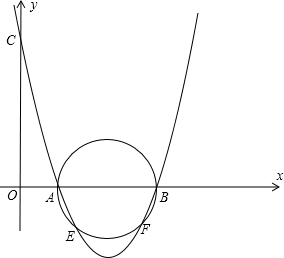 已知抛物线经过点A(1,0)、B(3,0)、C(0,3),以AB为直径画圆.
已知抛物线经过点A(1,0)、B(3,0)、C(0,3),以AB为直径画圆. 如图,已知抛物线经过点A(-3,0),B(0,3),C(2,0)三点.
如图,已知抛物线经过点A(-3,0),B(0,3),C(2,0)三点.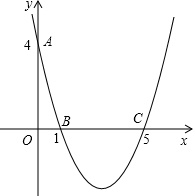 如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.
如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.