Question

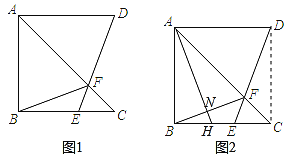
【题目】如图，在平面直角坐标系中，正方形ABCD的顶点A的坐标为（﹣1，1），点B在x轴正半轴上，点D在第三象限的双曲线y上，过点C作CE∥x轴交双曲线于点E，则CE的长为（　　）

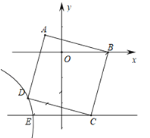
A. 2.5B. 3C. 3.5D. 4

Answer 1

【答案】C

【解析】

证明△DHA≌△CGD（AAS）、△ANB≌△DGC（AAS）得到：AN=DG=1=AH，而AH=-1-m=1，解得：m=-2，即可求解．

设点D（m，），

如图所示，过点D作x轴的垂线交CE于点G，过点A过x轴的平行线交DG于点H，过点A作AN⊥x轴于点N，

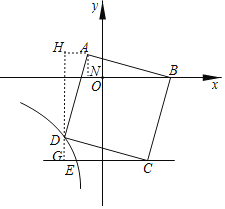
∵∠GDC+∠DCG=90°，∠GDC+∠HDA=90°，

∴∠HDA=∠GCD，

又AD=CD，∠DHA=∠CGD=90°，

∴△DHA≌△CGD（AAS），

∴HA=DG，DH=CG，

同理△ANB≌△DGC（AAS），

∴AN=DG=1=AH，则点G（m，-1），CG=DH，

AH=-1-m=1，解得：m=-2，

故点G（-2，-4），D（-2，-3），H（-2，1），

则点E（-，-4），GE=，

CE=CG-GE=DH-GE=4-=3.5，

故选C．